论文1：Do We Really Need to Access the Source Data? Source Hypothesis Transfer for Unsupervised Domain Adaptation

文章题目是《我们真的需要访问源数据吗？ 无监督域适应的源假设迁移》，发表在ICML2020，目前citation 382。

code:https://github.com/tim-learn/SHOT

Motivation

  • 之前的无监督域适应的方法需要接入源域的数据进行适应，在分布式或者数据不共享场景会造成私有数据的泄露。

Contributions

  • 论文的假设是有标签的源域数据经过训练好的特征提取器，输出的特征和分类器的结果应该和无标签的目标域数据输出的特征是对齐的，分类器的结果是相似的；
  • 为了实现特征对齐，从信息论的视角，文章利用自熵最小化和网络输出类别比较平均两个方面进行约束，来使得信息最大化；
  • 为了防止分类器输出噪声结果的影响，文中还在特征层面，对目标域的特征输出通过原型聚类生成伪标签，来约束目标域的训练。

做法

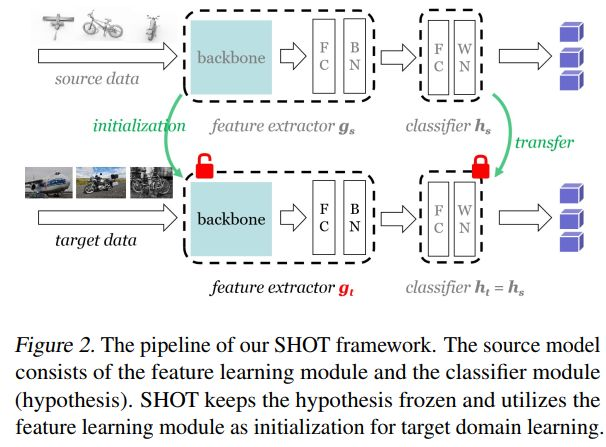
zxsDYD.png

步骤

  • 在有标签的源域数据上，训练一个特征表示器和分类器；

  • 在无标签的目标域数据上，冻结分类器，用entropy loss和diversity loss约束目标域的特征调整backone参数；

  • 更新伪标签。

    利用softmax对特征进行加权平均，再更新每一类的原型质心。根据调整后的原型得到的特征，再经过分类器计算伪标签。

损失函数

训练源域的损失函数，使用带有label smoothing的交叉熵；
zxWJNq.png

训练目标域的损失函数如下：

  • 使用分类器输出的K维向量进行自熵约束和互信息约束和伪标签交叉熵的约束。

    自熵最小化可以使得输出的预测类别更加确定，每个类别中的所有样本特征的均值最小化可以保证每个类别在特征空间中比较均匀。
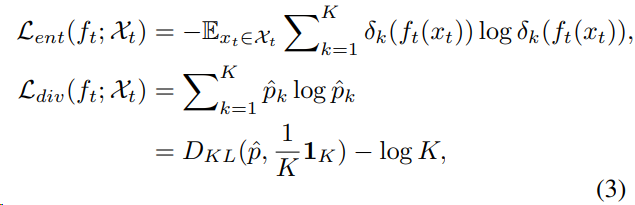
zxfiGV.png zxfQG6.png
  • 伪标签$\hat{y}_t$尖使用原型聚类来确定。
zxf8MD.png

总的损失函数为

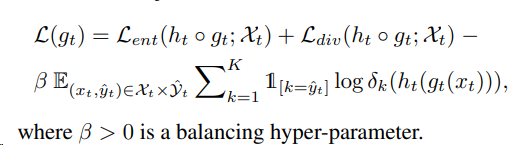
zxfNdA.png zxfdit.png

参考

https://blog.csdn.net/qq_39456088/article/details/117002227

论文2：Domain Adaptation without Source Data

文章题目是《没有源域数据的域适应》，发表在TAI（IEEE Transactions on Artificial Intelligence）2021，目前citation 62。和论文1是同期工作，对于无源域适应(Source data-Free Domain Adaptation, SFDA)，论文故事讲的好。

code:https://github.com/youngryan1993/SFDA-SourceFreeDA

Motivation

  • 不同域之间会存在数据不共享或者信息敏感的问题，目标域只能获得预训练的源域模型，无法获得其数据。
  • 论文观测到，在无标签的目标域上，不是所有数据都适合用于进行源域适应，只有在预训练的源域模型得到的自熵值较低的样本才是可靠的（熵值越小，不确定性越低），可用于目标域的训练。

Contributions

  • 为了减少源域适应时伪标签的不确定性，文章从度量学习的视角出发，提出基于豪斯多夫距离的过滤来筛选出自信样本，并且该距离是自适应的。
  • 训练目标域模型时，文章通过预训练的源域模型和根据距离过滤得到置信度较高的伪标签进行双重约束。

做法

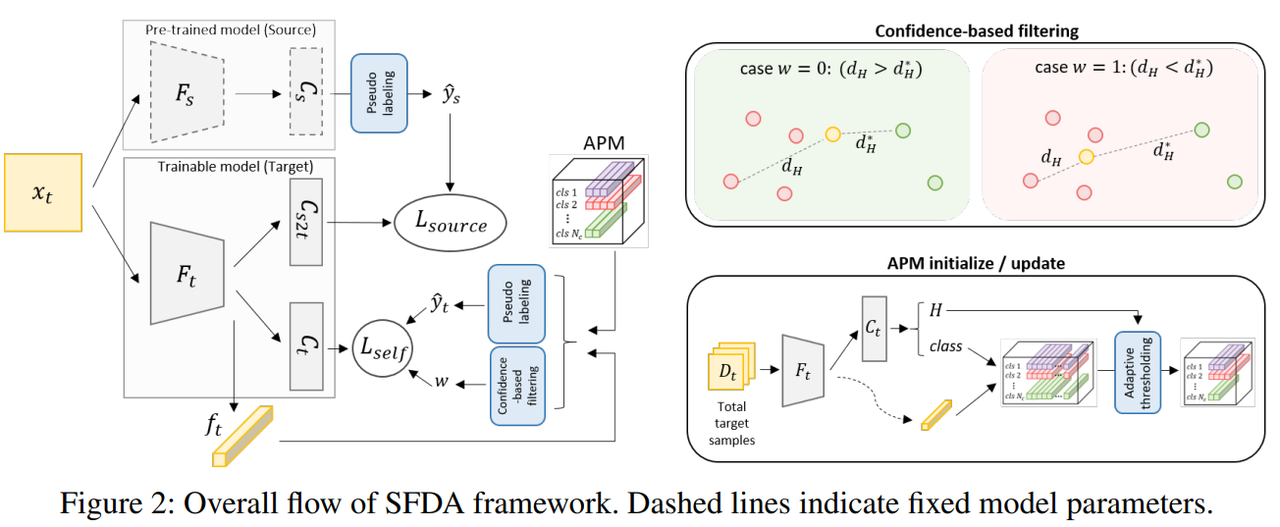
zxIkk9.png

算法流程图

zxIm6K.png

步骤

利用预训练的源域模型的主干网络$F_s$和分类器$C_s$去初始化目标域模型的主干网络$F_t$和两个分类器$C_t$、$C_{s2t}$。文中通过预训练模型的分类结果作为伪标签去约束目标域模型。此外，文中还通过不断更新自适应的原型记忆和每个目标域样本特征子集到原型子集的豪斯多夫距离进行度量。

  • 自适应的原型记忆(Adaptive prototype memory, APM)

    选择目标域数据中每一类别，归一化自熵最小的样本作为一个集合，选择集合中最大的熵值作为定义多个原型$M_c$的阈值。由于计算一次原型开销比较大，文中设置100个steps周期计算更新APM。

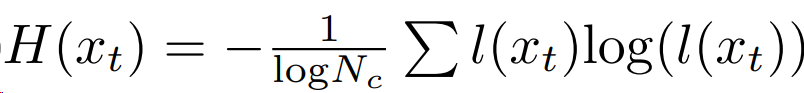
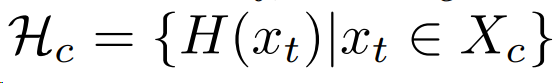
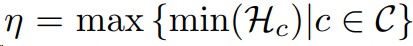
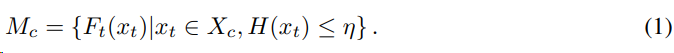
    zxo93t.png zxoPjf.png zxoAHg.png zxoVEQ.png

  • 置信度的过滤出目标域的可靠样本（Confidence-base filtering, CD filtering）

    • 原型embedding和目标域样本特征之间的相似度为
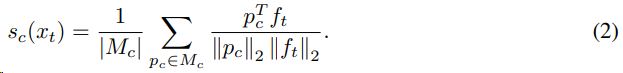
      zxoKg0.png

      通过极大似然估计找到当前目标域样本最相似的类别。

      zxoJUJ.png

    • 目标域样本特征子集$Q$和原型特征子集$p$之间使用豪斯多夫距离度量，并使用上确界和下确界优化为最大最小值问题，进而度量出原型$M_c$中最相似的类$M_{t1}$和第二相似的类$M_{t2}$。

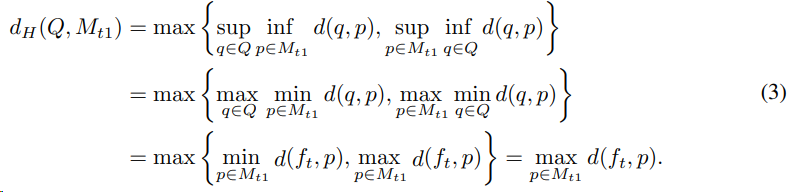
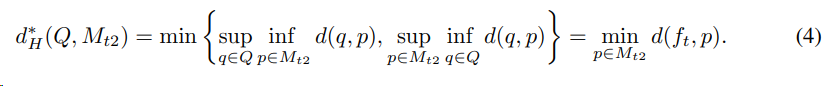
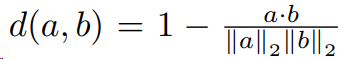
      zxTSZF.png zxT9IJ.png zxTFR1.png

      基于上述距离的定义，可以指定样本选择策略为

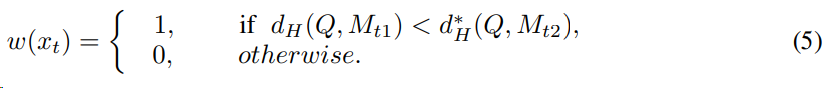
      zxTJL8.png

损失函数

预训练的源域模型进行伪标签的约束为

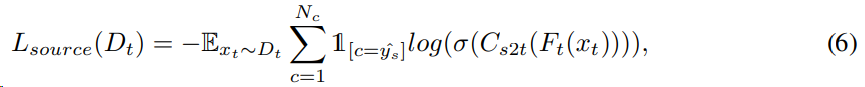
zxTrQ0.png

通过APM中的原型特征空间度量出置信样本的损失为

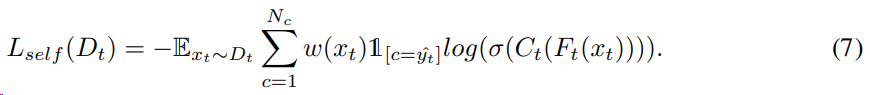
zxTyLT.png

总的损失函数为

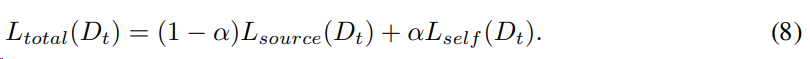
zxTceU.png

论文3：Source-Free Domain Adaptation via Distribution Estimation

文章题目是《通过分布估计进行无源域数据的域适应》，发表在CVPR 2022，目前citation 4。

code:无。

传统的域适应的方法是假设源域和目标域的数据都是可获得的。无源域适应（Source-Free Domain Adaption, SFDA）指在数据不共享的场合，可以通过源域的预训练模型和目标域的数据进行跨域知识迁移。

Motivation

  • 目前的SFDA的方法（SHOT:通过最大化互信息和最小化熵来隐式对齐两个域；G-SFDA:通过生成更多目标域的数据来学习目标域的分布；A2Net:通过引入新的分类器利用对抗学习来对齐两个域；SoFA:利用变分自编码器来建模目标域数据的分布。）没有对齐源域和目标域的特征分布来进行域适应。
  • 许多SFDA的做法是冻结源域的分类器，根据目标域的数据对齐分类器输出的伪标签。本文也是在此基础上，旨在探究更鲁棒的伪标签生成策略和两个域之间的特征对齐方法。

Contributions

  • 对于通过源域预训练模型得到的目标域的特征，使用更鲁棒的伪标签策略（Spherical K-Means聚类）；
  • 提出源域分布估计（Source Distribution Estimation ， SDE）来逼近源域分布，假设源域和目标域的特征的语义信息是一致的，再从逼近的代理分布中采样出代理特征，来使得目标域进行和估计的源域分布进行对齐，从而适应源域模型的分类器。用代理源域分布取代源域分布，把无源的问题转化为有源。

做法

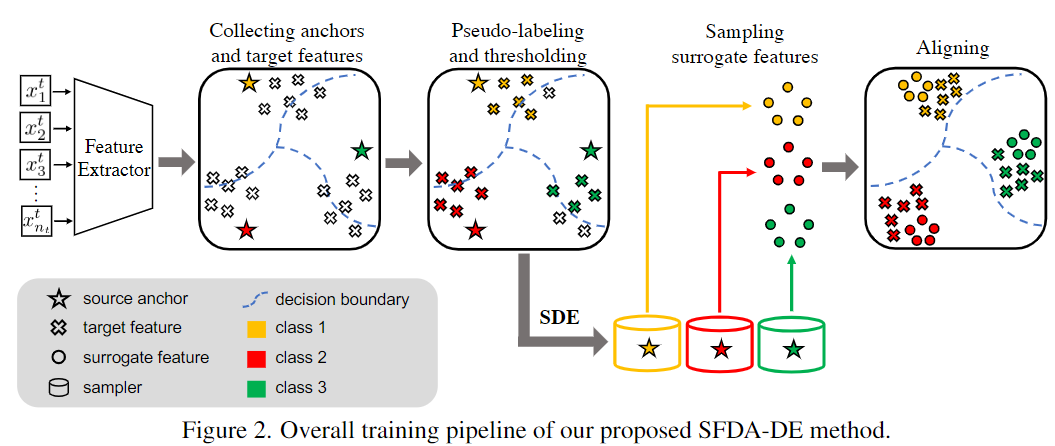
zzPgv8.png

算法流程图

zzPOrF.png

步骤

  • 根据source anchors和spherical k-means clustering来获得鲁棒的伪标签
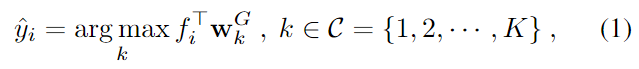
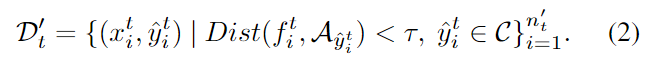
    • 目标域的数据经过预训练的源域模型后，对特征进行球形K-Means聚类（超球面利用余弦距离聚类），聚类中心作为source anchors，设置阈值$\tau$进行进行聚类迭代。zzPxa9.png zzPz5R.png

  • 源域分布估计

    • 假设源域的特征服从“类条件多元高斯分布”，$f^s_{i,k}∼N^s_k(μ^s_k,Σ^s_k)$。利用一个代理分布$N^{sur}_k(\hat{μ}^s_k,\hat{Σ}^s_k)$去逼近未知的源域特征分布；

    • 估计代理分布的均值。使用锚点和目标域的特征均值 $f^t_k$和锚点来估计$\hat{μ}^s_k$；

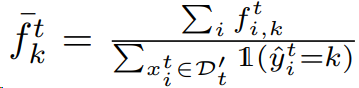
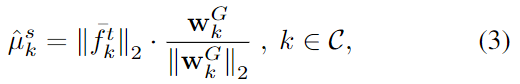
      zzi2J1.png zziRRx.png

    • 估计代理分布的方差。假设源域和目标域的特征的语义信息是一致的，可以利用目标域的统计特性配上采样范围$\gamma$进行估计源域的方差。

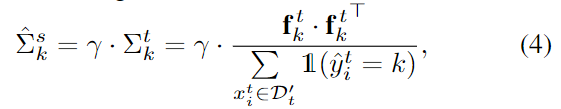
      zzFUTH.png

      得到代理分布算是模拟源域特征的分布。

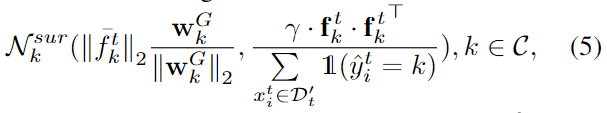
      zzF5pq.png

  • 无源域适应

    • 从代理分布中采样出源域数据的特征，把无源域适应问题转化为传统的DA问题。

    • 使用MMD(Maximum Mean Discrepancy, MMD，度量两个分布在再生希尔伯特空间的距离。MMD的基本思想就是，如果两个随机变量的任意阶都相同的话，那么两个分布就是一致的。而当两个分布不相同的话，那么使得两个分布之间差距最大的那个矩应该被用来作为度量两个分布的标准。)作为约束拉近代理源域的特征分布和目标域的特征分布的距离。$k_1$和$k_2$属于总类别中子类别的任意两个类，$f^{sur}$表示代理分布的特征。$n_b$为随机从代理源域分布中采样出$n_b$个特征。

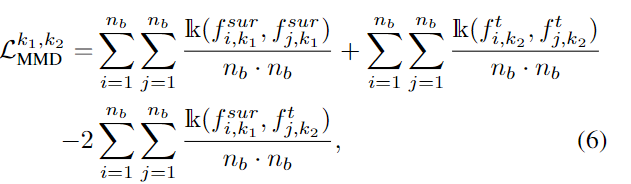
      zzkkAH.png

    • 通过对比域差异（Contrastive Domain Discrepancy, CDD)方法来显式对齐目标域特征的分布和估计源域的分布，即最小化类内域差异，最大化类间域差异。

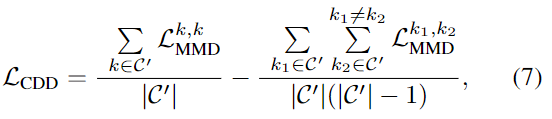
      pSCgvkj.png

参考

DA-5-Source-Free Domain Adaptation via Distribution Estimation_无CCFA就不改名的博客-CSDN博客