关于机器学习中的评价指标概念的问答。
分类模型常用的评价指标有?(分类模型的评价指标)
评价指标有
混淆矩阵
真实结果 预测为正例 预测为反例 正例 TP(真正例) FN(假反例) 反例 FP(假正例) TN(真反例) 矩阵的非对角线元素为0得到完美分类器。
准确率(Accuracy)和错误率(Error Rate)
- ACC:所有样本中预测正确样本的比例;
- Error Rate:所有样本中预测错误样本的比例。
$$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$
$$Error Rate=\frac{FP+FN}{TP+TN+FP+FN}=1-ACC$$
ACC和Error Rate缺点:测试类别极度不均衡时,无法反映算法的性能。
精确率(Precision)和召回率(Recall)
- 精确率(precision):预测为真时,正确的结果占预测结果的比例。
- 召回率(recall):预测为真时,正确的结果占真实结果的比例。
$$P=\frac{TP}{TP+FP}$$
$TP+FN$表示该类真实的样本数,查全率为
$$R=\frac{TP}{TP+FN}$$- 精确率(precision):预测为真时,正确的结果占预测结果的比例。
F1-score
当P和R出现矛盾,需要综合考虑时,可以使用F-Measure(F-Score),它是P和R调和平均的结果,公式如下。
$$\frac{1}{F_\beta}=\frac{1}{\beta^2}(\frac{1}{P}+\frac{\beta^2}{R})$$
当$\beta=1$时,也就是常见的$F1$度量,当$F1$越高,模型的性能越好。查准率和查全率的调和平均,比算术平均(求和除以2)和几何平均(平方再相乘开方)更重视较小值。ROC曲线
受试者操作特征曲线(Receiver Operating Characteristic curve, ROC)是以”假正例率”(False Positive Rate,FPR)为横坐标,”真正例率”(True Positive Rate, TPR)为纵坐标的曲线,其中TPR只和正例样本数据有关,FPR只和负例样本数据有关。所以ROC曲线不受正负样本比例的影响。
$$TPR=\frac{TP}{TP+FN}$$
$$FPR=\frac{FP}{FP+TN}$$
且FPR低的同时能有高的TPR(曲线越靠近左上角且越陡峭,模型越理想)。AUC(一般指ROC下的面积,也有PR_AUC)
曲线下的面积越大,模型性能越理想。KS曲线
FPR表示模型对于负样本误判的程度,而TPR表示模型对正样本召回的程度。KS曲线是TPR曲线和FPR曲线的最大间隔距离。
$$KS=max(TPR-FPR)\in[0,1]$$P-R曲线
宏平均和微平均
介绍下查准率/查全率/F1?
二分类问题在正反例类别不均衡时,acc作为评价指标则失去意义。此时可以考虑查准率和查全率。
查准率(precision):预测为真时,正确的结果占预测结果的比例。
查全率(recall):预测为真时,正确的结果占真实结果的比例。
举例:70张猫和30张狗的图像,经过某个分类器判断,得到50张猫和50张狗的输出。预测的50张狗的图像假设有30张是狗。此时总的准确率为$(50+30)/100=80%$,狗的精确率为$30/50=0.6$,召回率为$30/30=1$
用混淆矩阵表示如下:
| 真实结果 | 预测为正例 | 预测为反例 |
|---|---|---|
| 正例 | TP(真正例) | FN(假反例) |
| 反例 | FP(假正例) | TN(真反例) |
准确率定义为
$$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$
查准率为
$$P=\frac{TP}{TP+FP}$$
$TP+FN$表示该类真实的样本数,查全率为
$$R=\frac{TP}{TP+FN}$$
当P和R出现矛盾,需要综合考虑时,可以使用F-Measure(F-Score),它是P和R调和平均的结果,公式如下。
$$\frac{1}{F_\beta}=\frac{1}{\beta^2}(\frac{1}{P}+\frac{\beta^2}{R})$$
当$\beta=1$时,也就是常见的$F1$度量,当$F1$越高,模型的性能越好。查准率和查全率的调和平均,比算术平均(求和除以2)和几何平均(平方再相乘开方)更重视较小值。
介绍下P-R曲线?
P-R曲线描述的是查准率-查全率变化的曲线。
假设模型只输出正例的预测概率,对测试样本的预测结果进行降序排列,按降序的结果把每个预测概率作为区分正反例的阈值,以查全率为横坐标。查准率为纵坐标,从最小阈值和recall=1开始,从右往左绘制曲线,可得下图。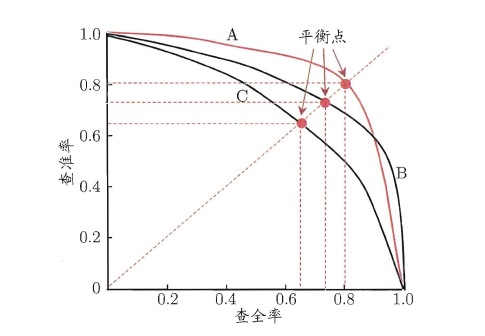
P-R曲线对模型性能的评估,一般可以通过P-R曲线下的面积大小(Area Under Curve, AUC)来估算,如果曲线有交叠,也可以通过“平衡点”(Break-Event Point, BEP)来估算。即当P=R时,平衡点的取值越高,模型性能越好。
如何理解宏平均和微平均?
- 宏平均(macro average):将每个类别的P、R、F单独计算,然后所有类别的指标直接取平均。
- 微平均(micro average):把所有类别都考虑进来,统计计算P、R、F。
如二分类中,
$$micro-P=\frac{TP1+TP2}{TP1+FP1+TP2+FP2}$$
在多分类的类别不均衡问题中,使用微平均的更关注少数类别。宏平均和微平均公式如下。

ROC曲线有什么优点?
PR曲线和ROC(Receiver Operating Characteristics)曲线对不平衡数据的表现不同。接受者操作特征曲线是根据混淆矩阵得到的。
- PR曲线对数据不平衡是敏感的,正反例的比例变化会使得PR曲线发生很大变化;因为P和R的计算依赖于不同类别。
- ROC曲线是以”假正例率”(False Positive Rate,FPR)为横坐标,”真正例率”(True Positive Rate, TPR)为纵坐标的,FPR和TPR的计算只依赖于统一类别数据内部。故ROC曲线对数据不平衡并不敏感。
AUC是什么?AUC是否对正负样本比例敏感?
PR曲线也存在AUC,但是一般所说的AUC(Area Under Curve)是指ROC曲线下的面积,ROC曲线的横坐标是FPR,FPR只关注负样本,与正样本无关,TPR只关注正样本,与负样本无关,所以对横纵轴进行积分当然也不会对正负样本比例敏感。
$$AUC=\int_{t=\infty}^{\infty}y(t)dx(t)$$
AUC的意义以及两种计算方式?
- 意义:正例预测为正的概率值大于反例预测为负的概率值的可能性。
- 计算方法:
- 绘制ROC曲线,计算ROC曲线下的面积;
- 计算样本中正例预测为正样本的概率值大于反例预测成负样本的概率值的个数,累加计数再除以总样本数。
AB test的原理?
《百面机器学习》
AB Test是为了验证新模型、新产品或者新算法是否有提升的测试方法。
- 离散评估无法完全消除模型过拟合的影响;
- 离散评估无法还原线上的工程环境;
- 线上系统的某些商业指标在离线评估中无法使用。
AB Test的主要方法是对用户进行分桶,分为对照组和实验组,分桶的过程中要保证桶内样本的独立性和采样方式的无偏性。对实验组的用户实施新模型,对对照组的用户实施旧模型。根据检验指标判断AB两个模型对象哪个方案效果更好。


