Classification

概述

在机器学习中，分类问题是指给定一个输入，当输入经过某个模型后，输出判断该输入的所属类别。常见的应用有信贷评估（根据某人的收入、存款、职业、年龄等判断是否给他贷款），医学诊断（根据某人的性别、年龄和目前症状判断他患上哪一类型的疾病），手写体的识别和人脸识别。

案例：划分宝可梦的种类

在本例中，我们已知宝可梦具有18种类型（如下图，水系，雷系，草系等等），我们的任务是找到一个模型，使得输入一个宝可梦，输出是它的所属类型。

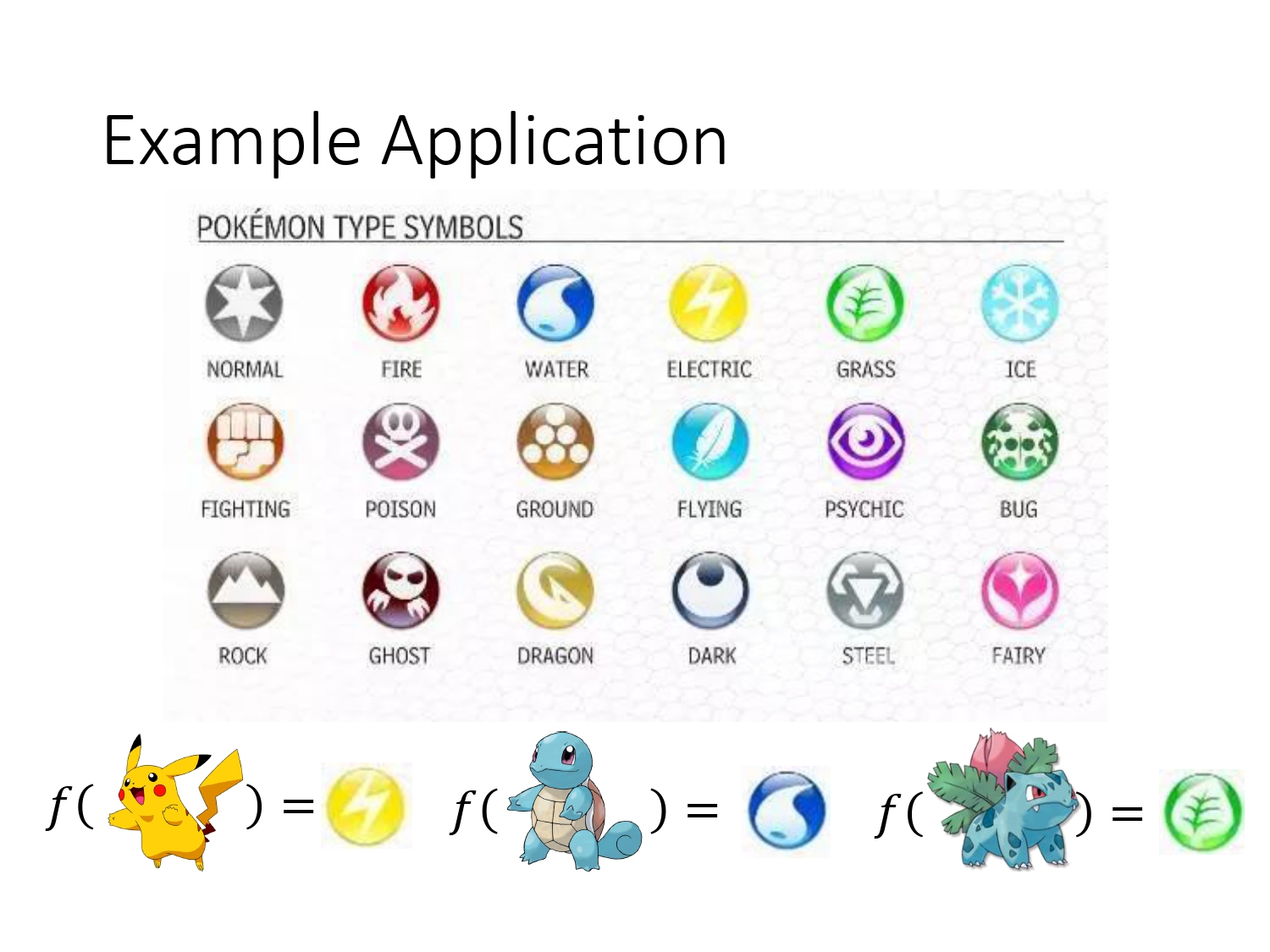
划分宝可梦分类这件事有什么意义呢？由下图可知，不同类别的宝可梦存在着相互制约的关系，当在决斗时，对手派出一个从未见过的宝可梦时，一旦我们能成功把它分对类，就可以按照下图派出能克制住它的宝可梦。从而百战不殆。

输入

明确我们的任务后，首先开始采集数据，即宝可梦的特征。如下图所示。

比如一只皮卡丘有7个特征(HP、Attack、Defense、SP atk、SP def等等)，这七个特征可用一个向量来描述。我们下一步要做的事是将数据输入到一个函数里，输出是某个种类的宝可梦。

建模

为简单起见，本例先描述二分类问题。

回归模型

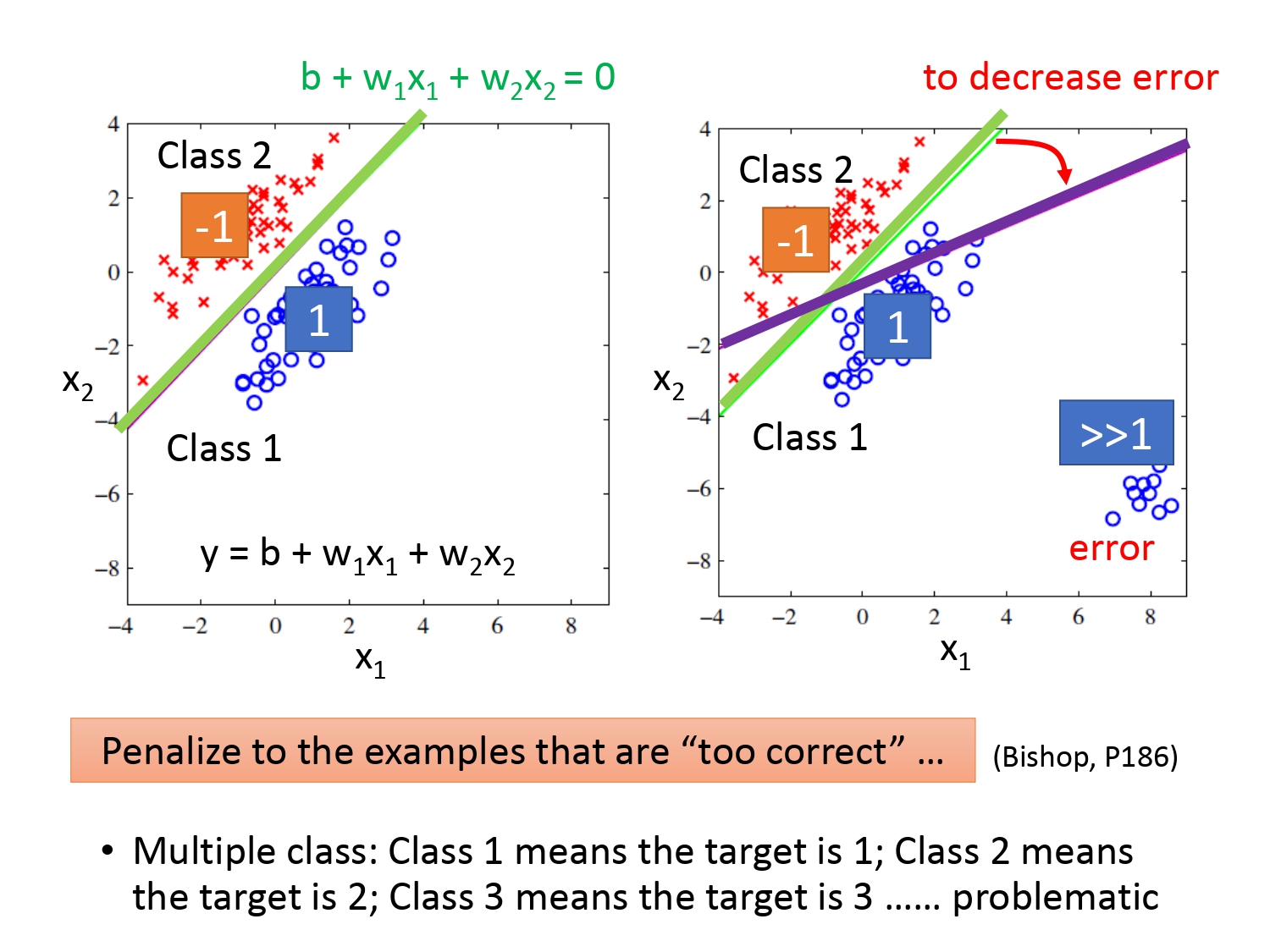
能不能采用Regression的方法进行二分类呢？如下图所示，我们假设类别1 的宝可梦的目标值是1，类别2的宝可梦目标值是-1，两种类型输出越靠近目标值越好。

如果恰好数据分布如下图左所示，我们确实能将二者分类并且效果不错，分界线就是绿线$y=b+\omega_1x_1+\omega_2x_2$，但如果蓝色数据的分布是下图右所示，比起左图，它存在了一些目标值远大于1的样本，这个时候我们是没有办法通过Regression训练得到绿色的线，只能得到紫色的线。为什么会这样呢？因为Regression的最终目标是使得$Loss$函数最小，为了达到这个目标，它会更偏向于靠近离群点方向。它认为紫色的线才是最好的函数。

可见Regression和Classification的目标是不一致的，所以采用回归的方法去解决分类问题是不适用的。并且在面对多分类问题时，如果我们把类别1的目标值设定为1，类别2的目标值设定为2，目标3 的目标值设定为3，这样的话由于1、2、3数值的设定而默认了类别1和类别2有关系（因为在数值上，1和2的距离比1和3更近），但实际上种类之间是没有关系的。所以采用Regression的方法不可靠。

概率模型

既然不能采用Regression的通用方法，比较理想的做法如下。

其中建模时对于二分类问题，一种可能的想法是在$f(x)$中内嵌一个函数$g(x)$，根据$g(x)$的正负判断输出的类型。损失函数$L(f)$的定义为在训练集中预测分类错误的次数之和，怎么找出最小的$Loss$函数呢？由于$L(f)$不可微分，所以不能采用梯度下降的方法，可使用感知机（Perceptron）或SVM（支持向量机）。但今天主要从概率学的角度介绍另一种方法。

分类原理

假设有两个盒子，各装了5个球，还得知随机抽一个球，抽到的是盒子1的球的概率是 $\frac{2}{3}$，是盒子2的球的概率是$\frac{1}{3}$。从盒子中蓝色球和绿色球的分配可以得到：

在盒子1中随机抽一个球，是蓝色的概率为 $\frac{4}{5}$，绿色的概率为 $\frac{1}{5}$
在盒子2中随机抽一个球，是蓝色的概率为$\frac{2}{5}$，绿色的概率为 $\frac{3}{5}$

现在问抽到一个蓝球，它属于盒子1的概率？

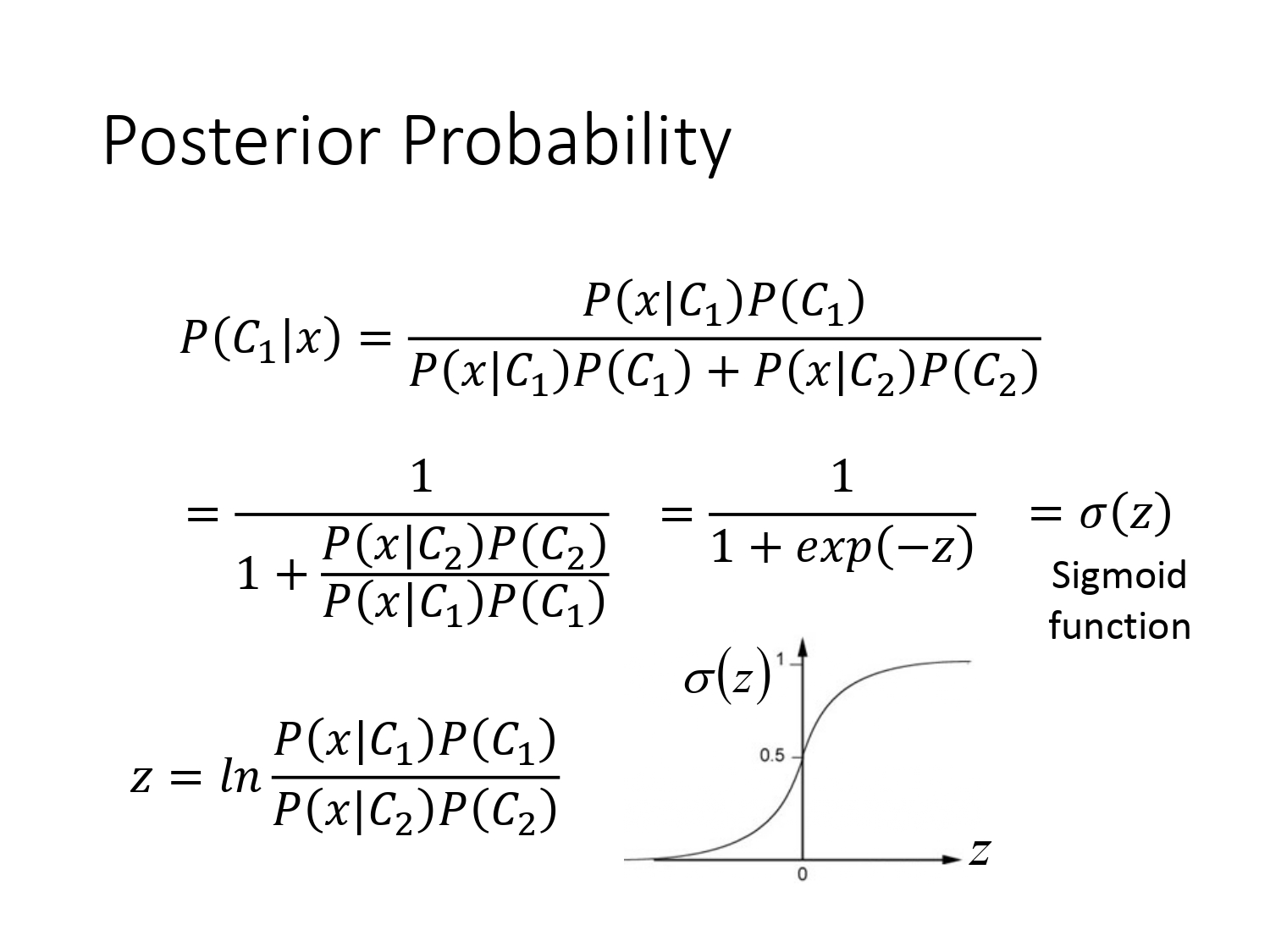
如上图所示，我们已知盒子1条件下是蓝球的概率，盒子2条件下是蓝球的概率，盒子1和盒子2各自的选取概率。根据贝叶斯公式可以求得后验概率（Posterior Probability）$P(B_1|Blue)$，即抽到是蓝球条件下属于盒子1的概率。

概率与分类的关系

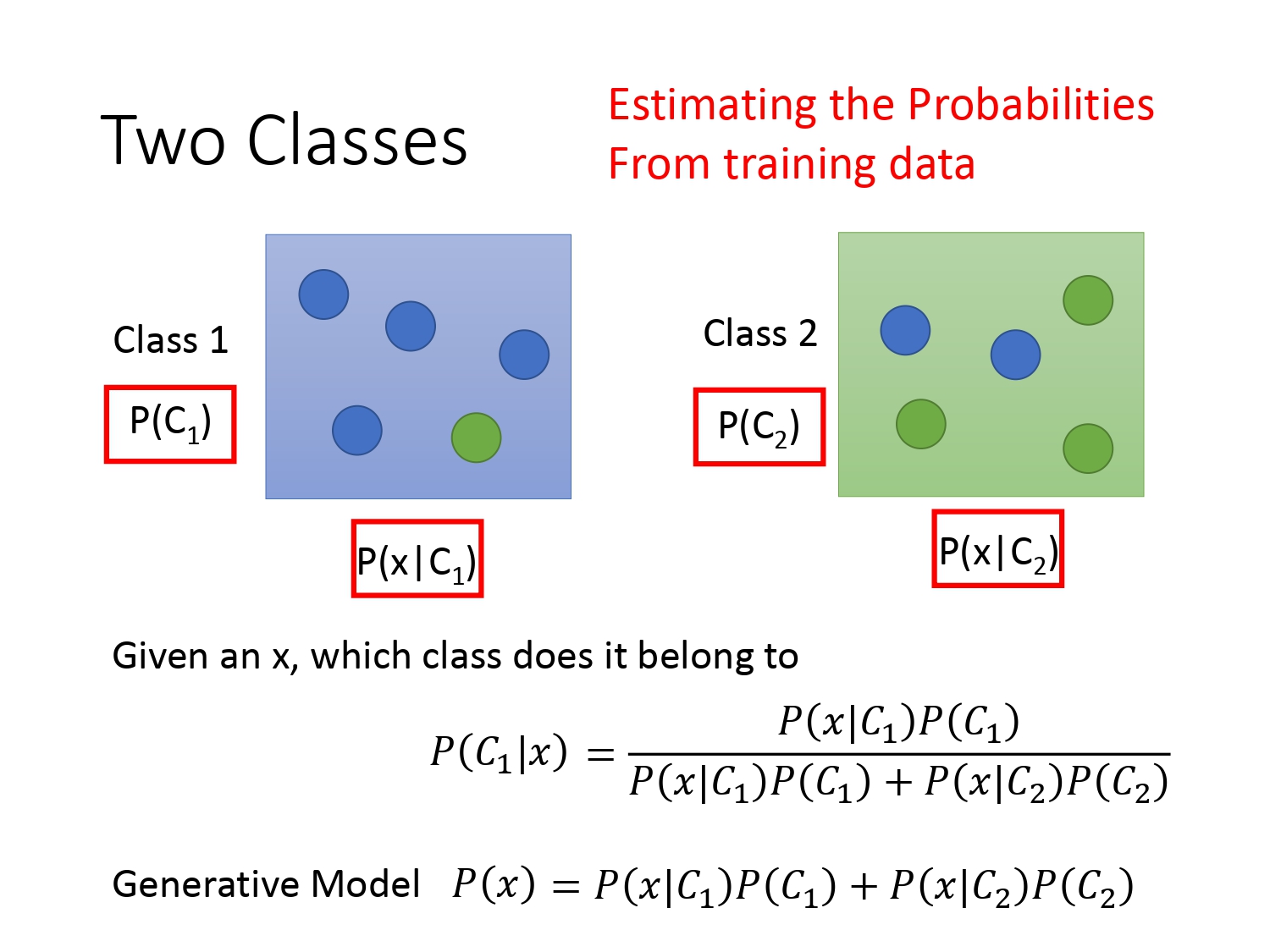
那上面的例子和分类有什么关系呢？这时我们把盒子1 换成类别$C_1$，把盒子2换成类别$C_2$，把蓝球换成我们要分类的样本$x$，同理如果我们已知下图红框的4个概率，根据贝叶斯公式可以求出后验概率$P(C_1|x)和$$P(C_2|x)$。

所以对于分类问题，我们的做法就是在训练集中求出图下的四个概率，再用贝叶斯公式某类别的后验概率。根据概率的大小判断属于某个类别。这套想法叫生成模型（Generative Model），为什么叫生成模型呢？因为我们可以通过红框的四个概率计算得到$x$的全概率，也就是$x$的分布，知道分布后我们就可以生成$x$。

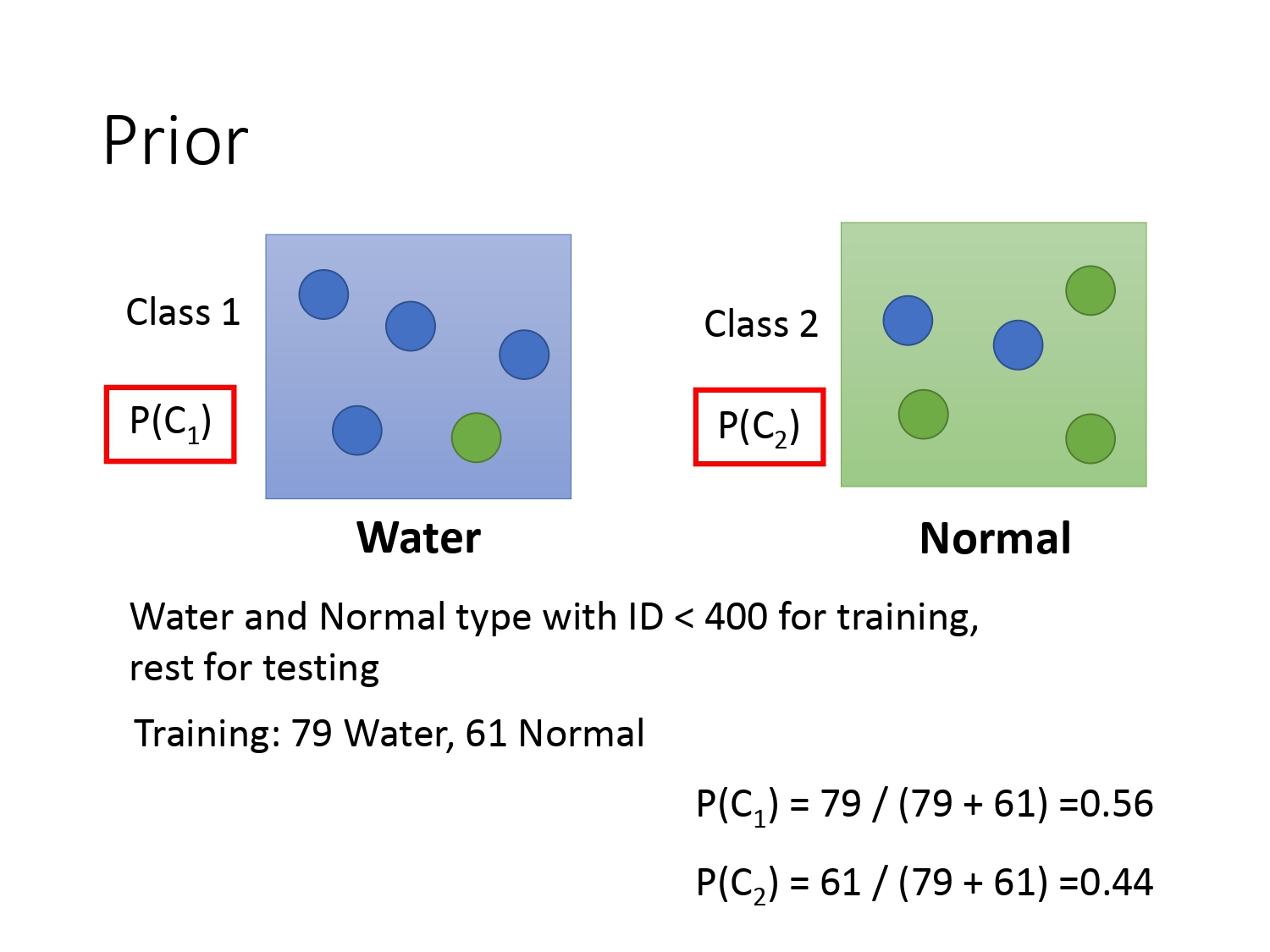
将生成模型运用到宝可梦的案例中，这里我们以二分类问题为例子，即宝可梦是属于水系还是一般系。训练集中总共79只水系的，61只正常系的。从水系中抽取一只宝可梦的概率和从正常系中抽出一只宝可梦的概率如下。

那么我们现在的问题是，抓到了一只原盖海龟$x$，它属于水系的概率$P(C_1|x)$多大呢？根据贝叶斯公式，我们还差$P(x|C_1)$和$P(x|C_2)$未知，但是在原来的水系里根本就没有海龟这个样本，如果令$P(x|C_1)=0$，显然不对。

由于在模型中，我们的输入是宝可梦的一系列特征，这里以宝可梦的Defense和SP Defense两个特征为例，将这79只宝可梦的两个特征可视化如下图所示。由于训练集的数据往往只是冰山一角，对于新样本的预测，数据必须服从某分布才能被预测。这里计算$P(C_1|x)$的前提是假设水系宝可梦的数据是服从一个高斯分布的。

高斯分布

高斯分布（Gaussian Distribution）的表达式如下所示。可知对于一个服从高斯分布的函数$f_{\mu,\Sigma}(x)$，只要确定了均值$\mu$和协方差矩阵$\Sigma$，就能够知道变量$x$的分布。（注：表达式中$D$是指向量的维度）不同均值$\mu$和协方差矩阵$\Sigma$代表的高斯分布也不同。如下两图是同一个$\Sigma$，不同$\mu$时的分布。

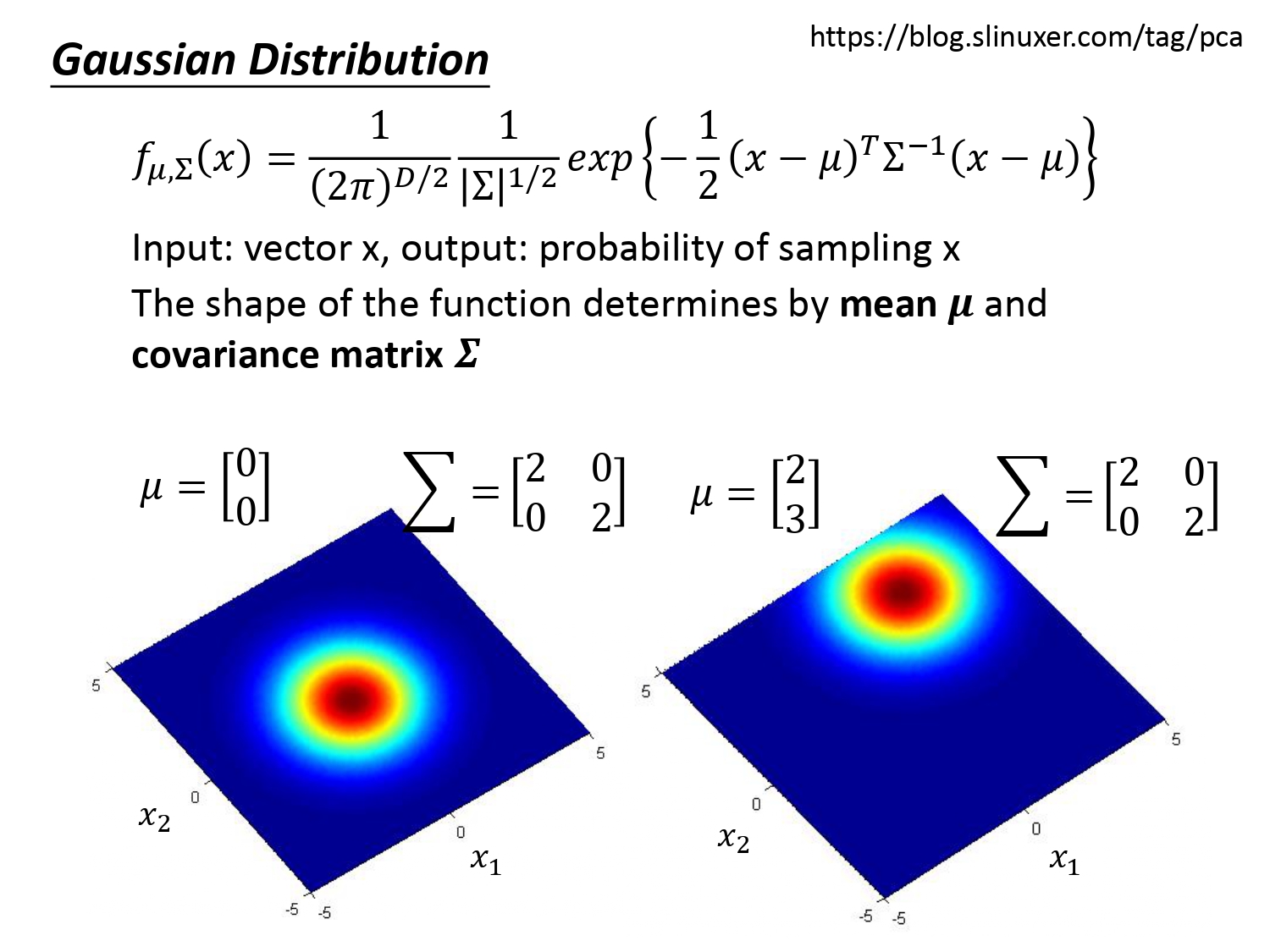
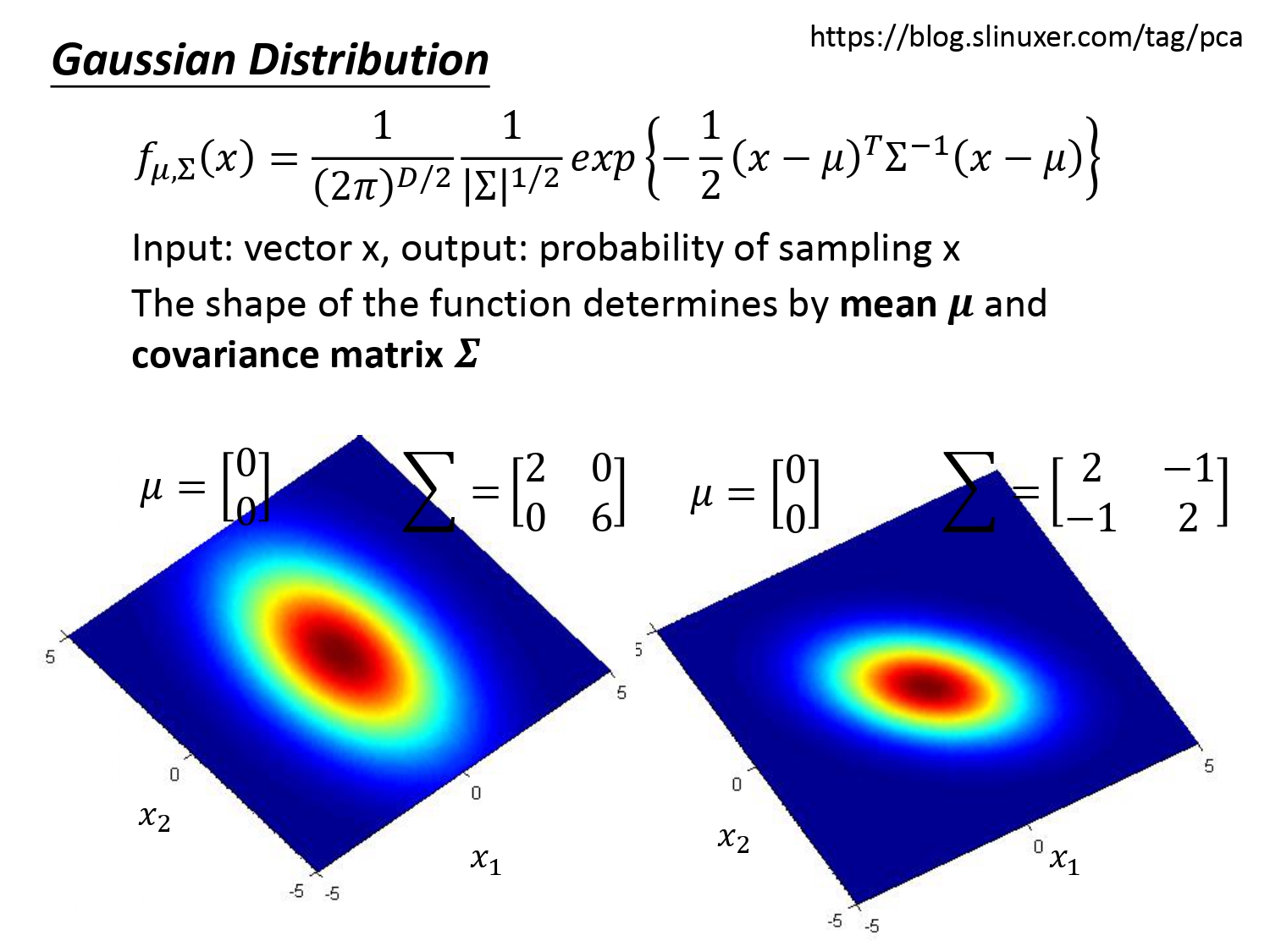
下两图是同一个$\mu$，不同$\Sigma$时的高斯分布。

其实对于宝可梦这79个样本点，任意确定均值$\mu$和协方差矩阵$\Sigma$都可以生成，只是它们生成每个点的概率大小不一样而已。如下图所示，对于靠左边的高斯分布生成这些点的可能性显然比右边的高斯分布要高。

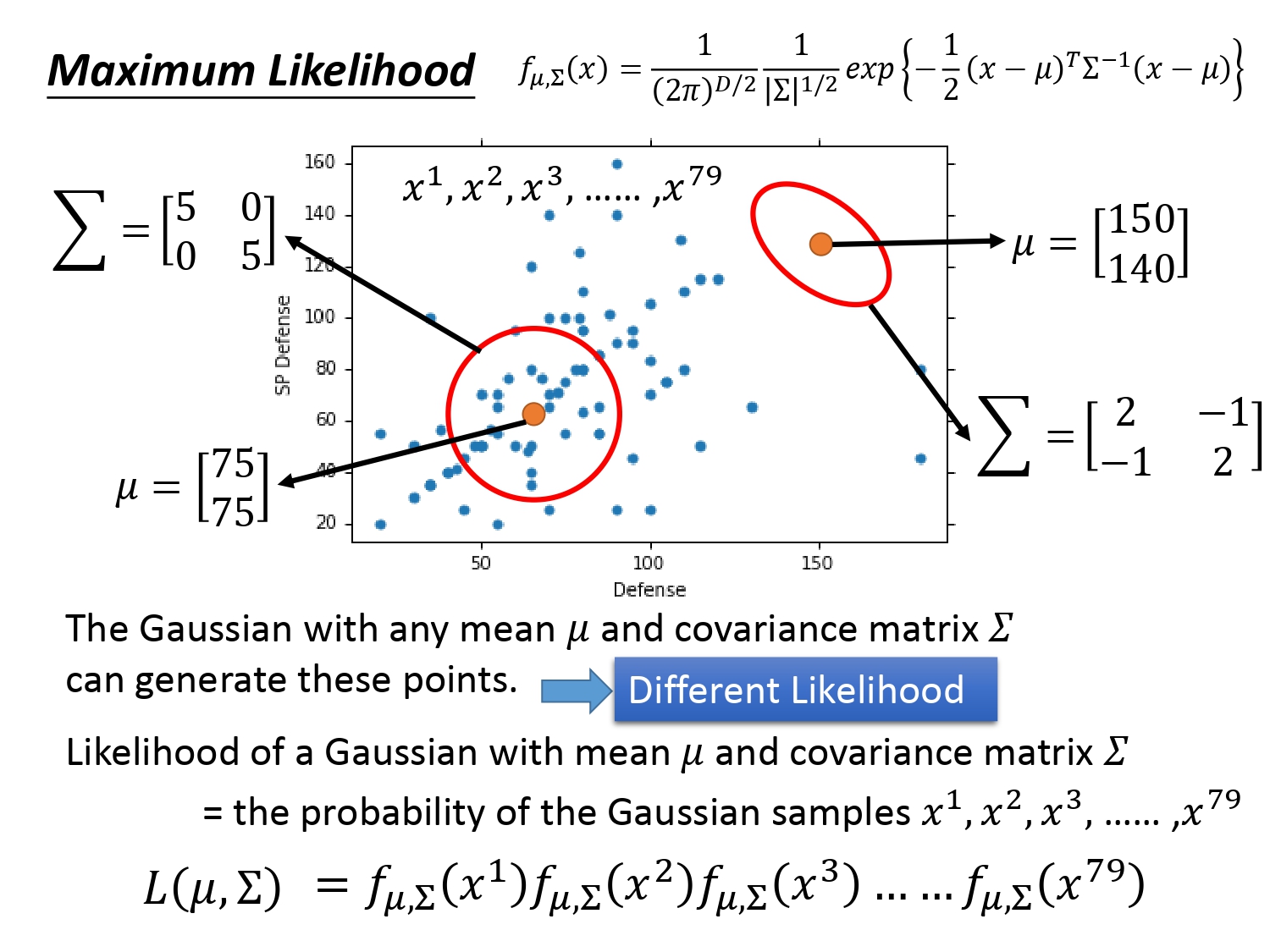
所以我们的任务变成了找一个最好的$\mu$和$\Sigma$，使得它们组成的高斯分布生成的各个采样点的概率最大。

最大似然估计

完成上述任务最直接的方法就是最大似然估计（Maxium Likelihood）,具体的做法时由于每个样本点都是独立采样的，对于给定的$\mu$和$\Sigma$，它们的概率记为下图中的$L(\mu,\Sigma)$，根据独立事件的定义可以将$L(\mu,\Sigma)$表示出来。$L(\mu,\Sigma)$也被称为样本的“似然函数”，接着要求使得似然函数$L(\mu,\Sigma)$值最大的$\mu$和$\Sigma$，记为$\mu^*$和$\Sigma^*$。

关于$\mu^*$和$\Sigma^*$值的计算，我们可以分别对$\mu$和$\Sigma$求偏微分，令偏导等于0可以得到下图的公式和结果。

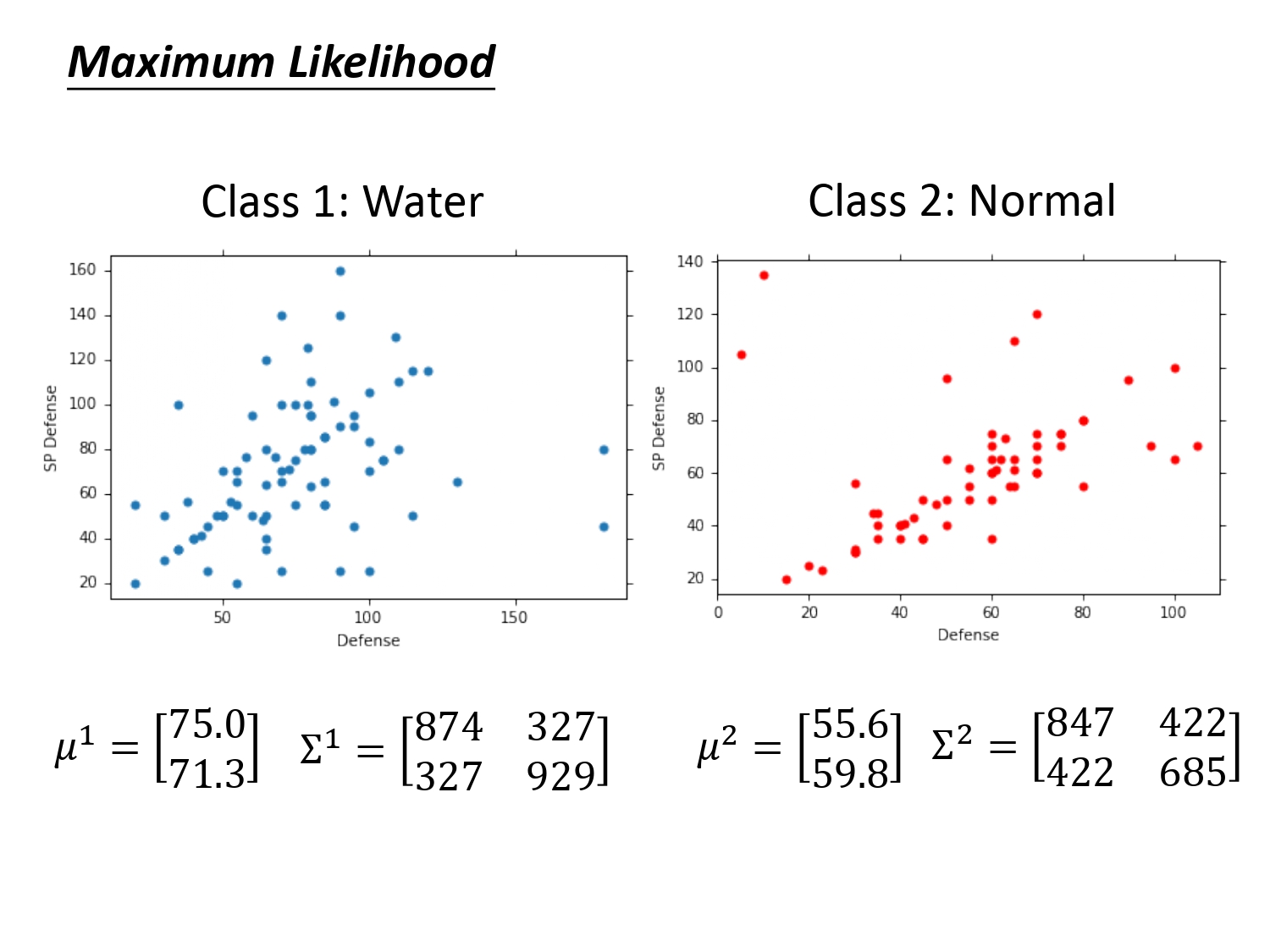
通过最大似然估计的方法，我们可以计算出两个系高斯分布的$\mu$和$\Sigma$，得到的结果如下。

分类结果

回到原来的问题，新来的原盖海龟$x$，它属于水系的概率$P(C_1|x)$多大呢？这下可以计算了。根据贝叶斯公式，我们要确定$P(x|C_1)$和$P(x|C_2) $ ，$P(C_1)$和$P(C_2)$，这四个值的大小计算如下。最后计算出结果$P(C_1|x)>0.5$，那它就属于水系。

根据宝可梦的Defense和SP Defense两个特征的分类结果如下。

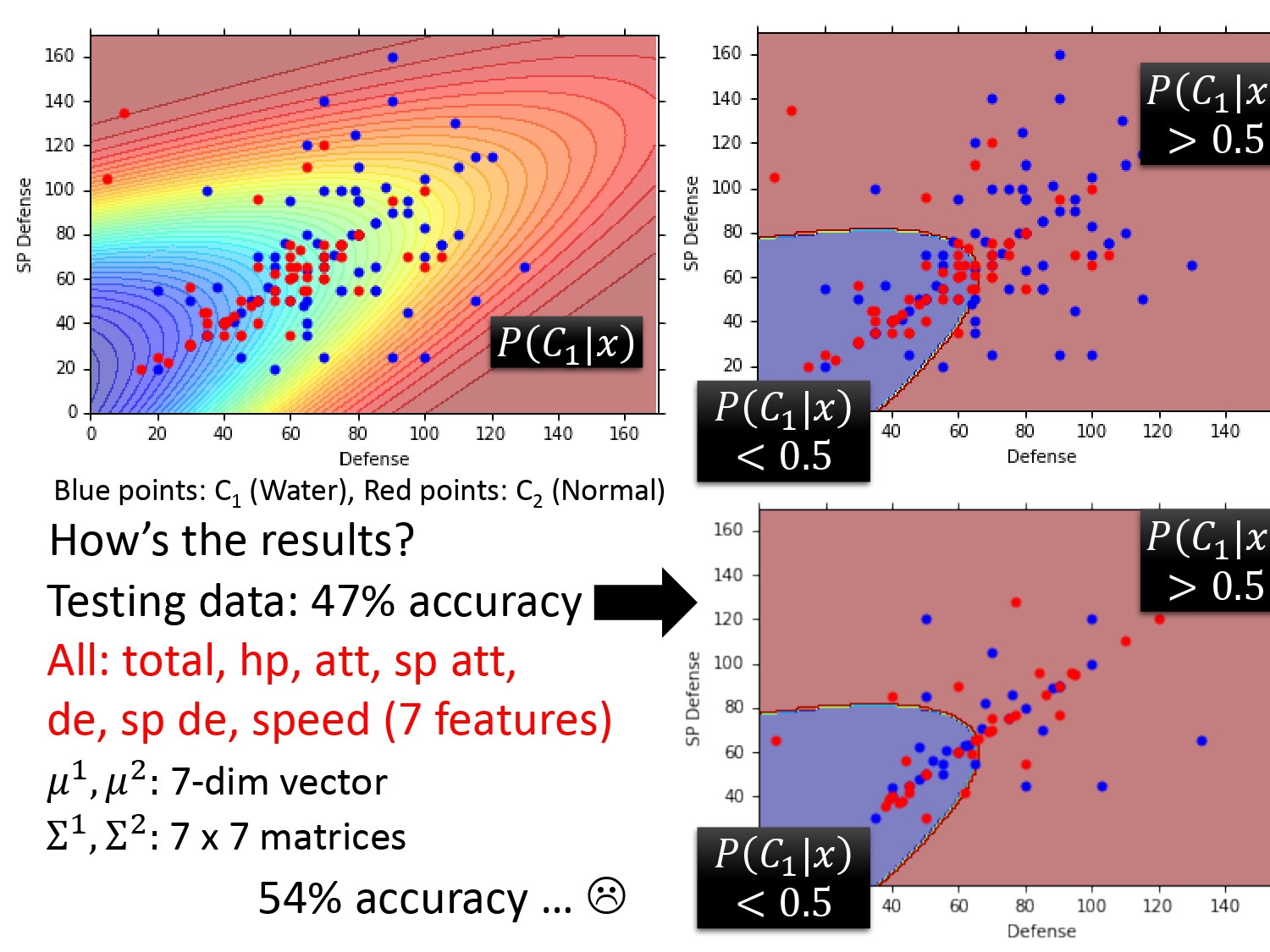
偏蓝部分是一般系的，偏红部分是水系的。可以看出只考虑这两个特征分类效果并不是很好，在测试集上的准确率只有47%。是不是因为我们考虑的特征太少了呢？在这里我们又把7个特征全考虑进去进行分类（当然7维空间图肯定画不出来，但计算机可以计算出来），最后在测试集上的准确度是54%，结果坏掉了。

最后归结原因为可能一般系和水系根本就没办法通过特征区分出来。或者是因为我们生成的协方差矩阵是$\Sigma^1$和$\Sigma^2$，协方差矩阵是和输入特征大小的平方成正比，所以当特征很大时，协方差矩阵是可以增长很快的。也就是模型的参数过多，这容易造成”过拟合”。

模型改进

改进方法

针对上述“过拟合”问题，我们对模型进行改进。思路是减少模型的参数，想法是共享两个高斯分布的协方差矩阵$\Sigma$。如下图所示。对于“水系”宝可梦，编码是1～79，服从的高斯分布均值为$\mu_1$；对于“一般系”的宝可梦，编码是80~140，服从的高斯分布均为$\mu_2$，它们的协方差矩阵都是$\Sigma$。

接着我们的任务是使用最大似然估计的方法计算使得似然函数$L(\mu_1,\mu_2,\Sigma)$最大的$\mu_1,\mu_2,\Sigma$。其中$\mu_1,\mu_2$的做法是和原来一样，而$\Sigma$的计算是原来$\Sigma^1,\Sigma^2$的加权平均。

改进结果

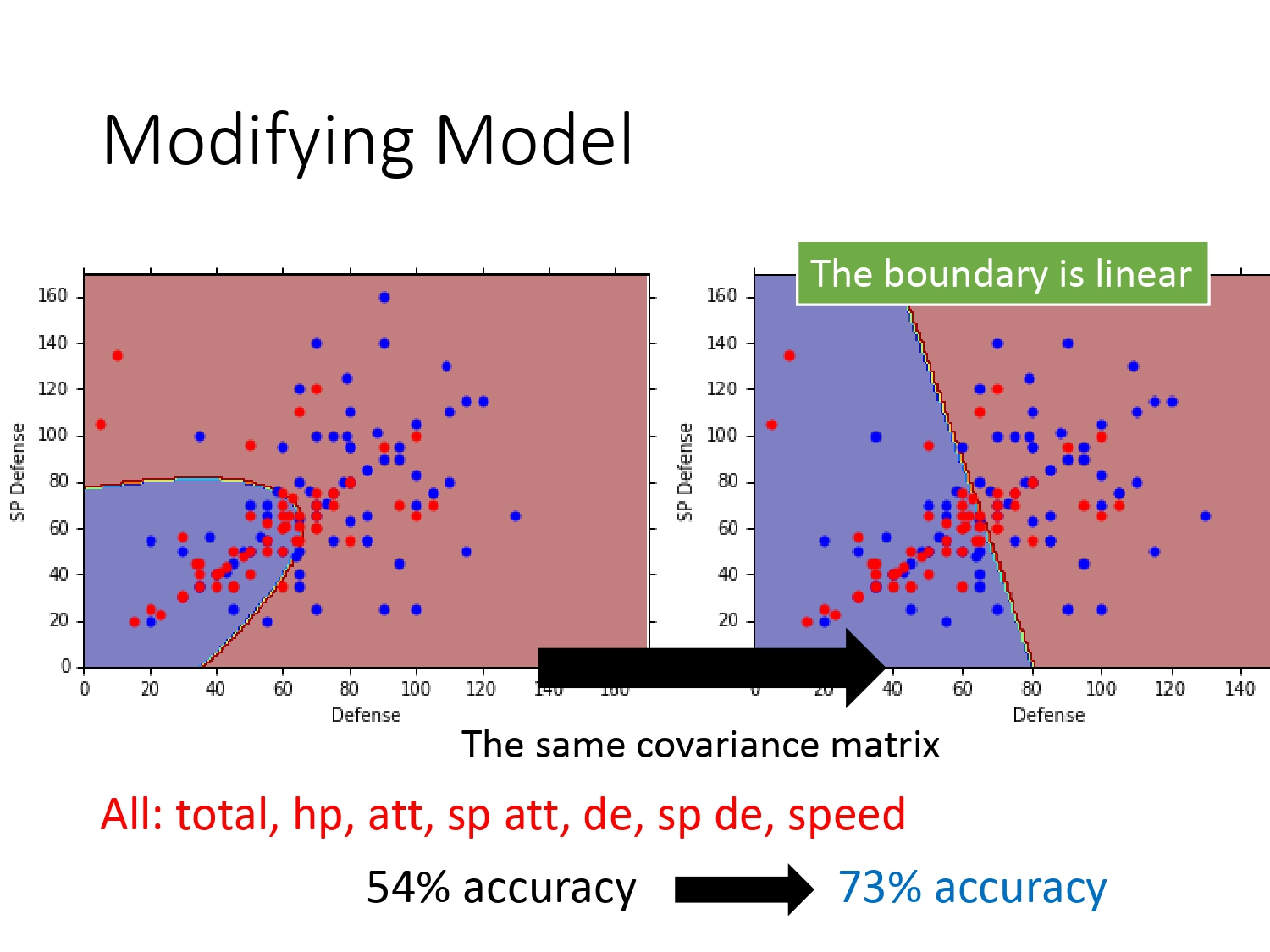
改进的结果如下所示。如果只考虑两个特征——SP Defense和Defense，输入空间是二维的。在我们从没有共享两个不同系的高斯分布协方差到共享它们的协方差矩阵，可以看出分界线也从曲线变成了直线。这种分类也称为“线性模型”。

但分类结果并不是很好（由于是二维空间，人眼就能看出分类）。如果考虑所有的7个特征，即输入空间是七维的。分类准确率从原来的54%提升到73%。所以说机器学习迷人的地方还在于它能处理高维度且人类无法直观想象的事情。

分类问题建模总结

在本例中，已经确定了使用概率模型和假设样本服从高斯分布。所以总结步骤如下。

四个先验概率通过贝叶斯公式计算出某一个样本的后验概率，根据概率值是否大于0.5进行分类；（建模）
如果遇到数据集中没有的样本$x$，我们可以假设所有的样本服从某一个分布，本例使用高斯分布，列出似然函数的式子；（找一个评价函数）
将已有数据通过最大似然估计法计算出最好的$\mu$和$\Sigma$，再求出样本$x$的四个先验概率进行分类。（选出最好的函数）

关于要怎样选择服从分布的问题，这主要依靠人去调节，具体问题具体分析。如果是二分类问题（判断宝可梦是不是神兽），此时可以选用二项分布（Bernouli Distribution）。如果恰好问题的各个特征之间都是统计独立的，此时可以使用朴素贝叶斯分类（Naive Bayes Classifier）。朴素贝叶斯分类的计算方法如下，假设问题的输入有$K$个特征，并且它们之间都是统计独立的服从一维高斯分布，最终先验概率的求解为各个特征的概率相乘。