这是我发的第一篇博客,抱着好玩的心态基于hexo搭建属于自己的网站,这里要非常感谢云游大大的云主题。关于机器学习的学习,今年5月份研究生上岸后开始接触,期间跟着B站台大李宏毅老师的课学习倒也写了四篇Markdown,后来到后面深度学习可写的东西太多了,果断不写了,学习它的思想。但是新博客还是要放点东西试试水的,空荡荡岂不很难受哈哈哈,以后更新尽量以总结性的为主。加油搬砖~
概述
在监督学习中,应用分为回归问题,分类问题和标注问题。回归问题一般是对连续值的处理,像预测房价,气温,销售额等。常用线性回归;分类问题模型一般输出是离散值,像图像分类,垃圾邮件识别,疾病检测等。常用softmax回归。所以回归应用场景十分广泛。
线性回归模型
为什么我们要对宝可梦的CP值(Combat Point的简称,属于战斗点数,CP值越高,战斗力越强。)进行预测呢?做这件事的理由是如果预测的宝可梦CP值较大,我们可以用它来进化,再去打道馆;如果预测的CP值小,我们就不用它进化而是做成宝可梦糖果。预测CP值的目的是为了节约资源和培养成本。
了解完动机后,我们该怎么预测呢?我们进行预测的前提条件是已经拥有一定数量的宝可梦的特征(像HP,进化前的CP值,weight,height,etc.)和它进化后的CP值。然后想办法(这里指回归)根据输入是特征和输出是CP值找到一个函数$f$,使得$f$尽量接近生成宝可梦CP值的函数。整个过程图形化如下图所示。
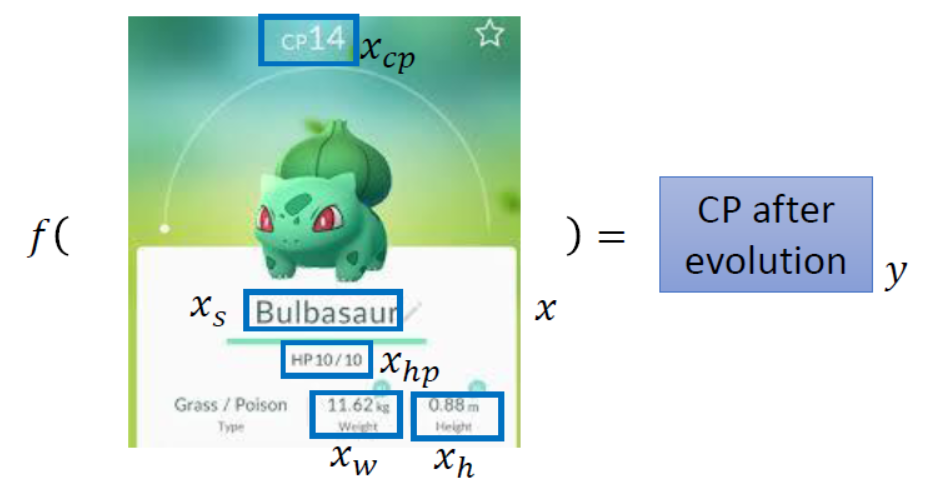
那怎么去找这样一个函数$f$呢?主要分为三步(第四步是计算):
本次主要采用线性回归的方法,设$y$表示宝可梦进化后的CP值,$y^n$表示第$n$只宝可梦进化后的CP值,$x_i^n$表示第$n$只宝可梦的第$i$个特征。$w$表示权重(weight),$b$表示偏差(bias)。
建模
如果我们只考虑进化前的CP这一个特征,则可建模为$y=b+\omega x_{cp}$,我们的任务是从一系列不同的$w$和$b$组成的函数集合找到一个最接近于目标函数(宝可梦的进化是按照某个函数来生成的)的函数$f$;
但是在实际求解时,我们一般还会考虑更多的特征。此时建模为$y=b+\sum w_{i}x_{i}$,($x_i:x_{cp},x_{hp},x_w,x_h$,……)我们的任务不变,还是是从一系列不同的$w$和$b$组成的函数集合中找到一个最接近于目标函数(宝可梦的进化是按照某个函数来生成的)的函数$f$;
计算损失函数
设$\hat y^n$表示第$n$只宝可梦进化后的真实CP值,$f(x_{cp}^n)$表示第$n$只宝可梦预测进化后的CP值,$x_i^n$表示第$n$只宝可梦的第$i$个特征。$w$表示权重(weight),$b$表示偏差(bias)。
为简单起见,以下谈论只考虑进化前的CP值这一个特征,则可建模为$y=b+wx_{cp}$,训练集是抓到的10只宝可梦,并且它们进化后的CP值已知。以进化前的CP值为横坐标,进化后的CP值为纵坐标。绘制成图为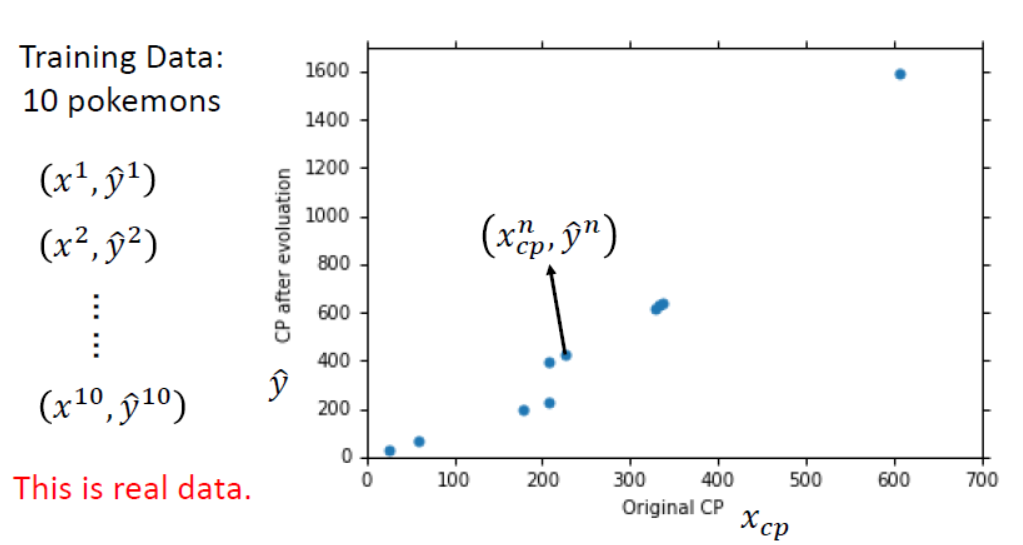
得到训练集数据和模型后,我们定义$Loss Function$(损失函数)为$L(f)$,它的输入是一个函数$f$,输出是判断的这个函数的好坏,其中$L$的值越小代表$f$越好。在本实例中定义为
$$ L(f)=\sum_{n=1}^{10}((\hat y^n-f(x_{cp}^n)))^2 $$
$w$,$b$代入,也就是
$$ L(w,b)=\sum_{n=1}^{10}(\hat y^n-(b+wx_{cp}^n))^2 $$
我们也可以把$b-w$的坐标轴画出来,观察下$w,b$对$L$的影响。如下所示。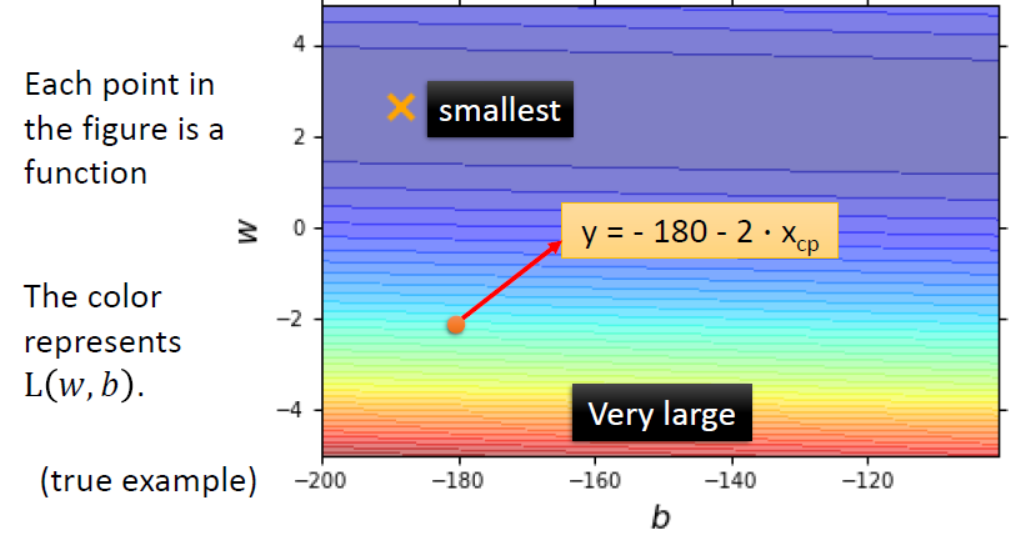
由图可知,红色部分$Loss$的值较大,$w$和$b$越偏蓝代表$Loss$的值越小,即函数的拟合性能越好。
找出使得损失最小的输入
损失函数值越小,说明函数的越接近目标函数。使损失函数最小的那个$w$和$b$就是最好的函数。即求解$f^*=\underset{x}{\operatorname {arg,min}}L(f)$
或为$$ w^*,b^*=\underset {w,b}{\operatorname {arg,min}}L(w,b)=\underset {w,b}{\operatorname {arg,min}}\sum_{n=1}^{10}(\hat y^n-(b+wx_{cp}^n))^2 $$
简单说就是求解能让$Loss$最小的$w$和$b$。如果学过线性回归的话,其实可以用最小二乘法进行求解出来。但是在李老师的课时,选用的是梯度下降(Gradient Descent)的方法来求解方程梯度下降的好处在于,不论损失函数$L$再复杂,只要它是可微的,都可以采用梯度下降来找到比较好的结果。
梯度下降的做法
那梯度下降具体的原理和做法是怎么的呢?本节暂时介绍做法,原理放在下一节讲。假设我们现在只考虑求解一个参数$w$的情况。
此时方程为$w^*=\underset {w}{\operatorname {arg,min}}L(w)$,假设$L(w)$的函数图像如下棕色线所示。我们的任务就变成了在一个“山峰”中找到最低点。具体做法是
(1)随机选取一点作为初始化的$w^0$;
(2)计算$\frac{dL}{dw}|_{w={w^0}}$;
(3)把$w^0-\eta\frac{dL}{dw}|_{w={w^0}}$的值赋给$w^1$进行更新。
$\eta$是人为定义的学习率,对$w$的值进行更新的目标是往$L$最小值的方向逼近,所以当计算微分值(斜率)为正时,要减小$w$的值;为负时要
增加$w$的值。并且增加量取决于微分值$\frac{dL}{dw}$和学习率$\eta$,相同微分值的情况下增大学习率,更新幅度大;减少学习率,更新幅度小。
(4)以上过程只走了一步,实际上想要到达最低点要不断地进行以上两步进行迭代,最后可能走到局部最优值(Local Minima)或全局最优值(Gobal Minima)。但是结果确实可能陷入局部最小值,这取决于初始化的$w^0$的位置。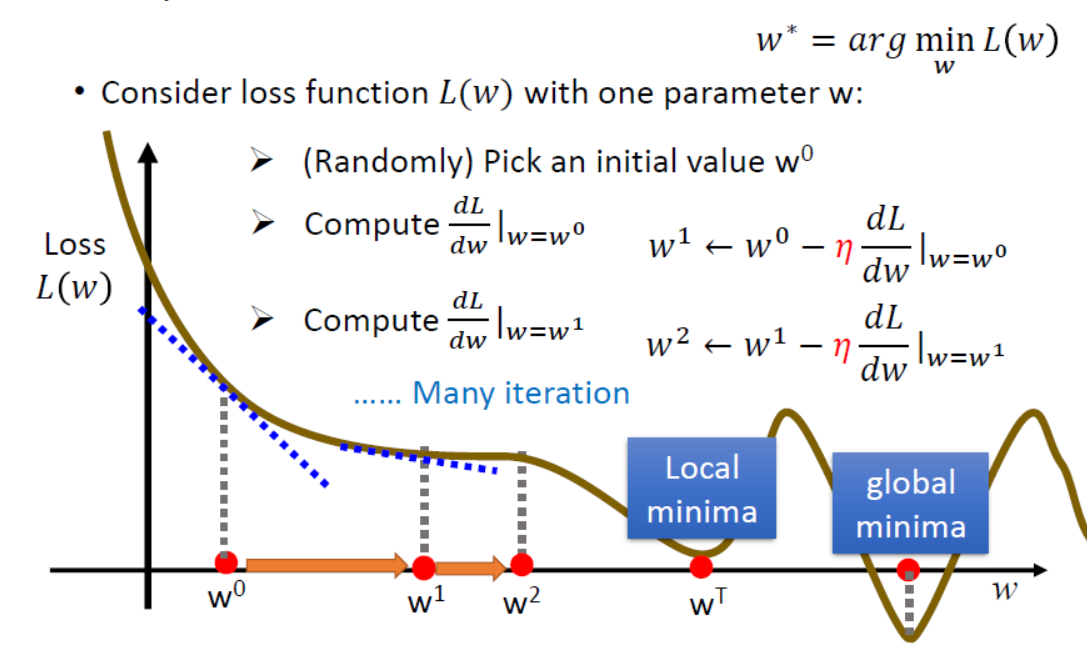
那回到原来的问题,当我们有两个参数$w,b$时,怎么进行梯度下降呢?
同理,做法雷同一个参数的情形,只不过变成了原函数对两个参数分别求偏导。具体做法如下PPT所示,在此不在叙述。
由两个参数的偏导数组成的矩阵就是函数$L$梯度。
梯度下降的过程可视化
梯度下降寻找最小值的过程如下。
其中$\frac{\partial{L}}{\partial{b}}$和$\frac{\partial{L}}{\partial{\omega}}$是曲线的法线方向,通过学习率$\eta$控制下一步走的前后方向,可见通过梯度下降,能不断在连续函数的某个区域中找到一个最小值,也就是图中的蓝色区域。
梯度下降可能遇到的问题
我们已经知道梯度下降方法是不管函数多复杂,只要它是可微的,总能求解出一个极值。那我们是否可以说经过多次更新参数后,我们都能得到最优的参数使得损失函数最小呢?不妨看下图的情况。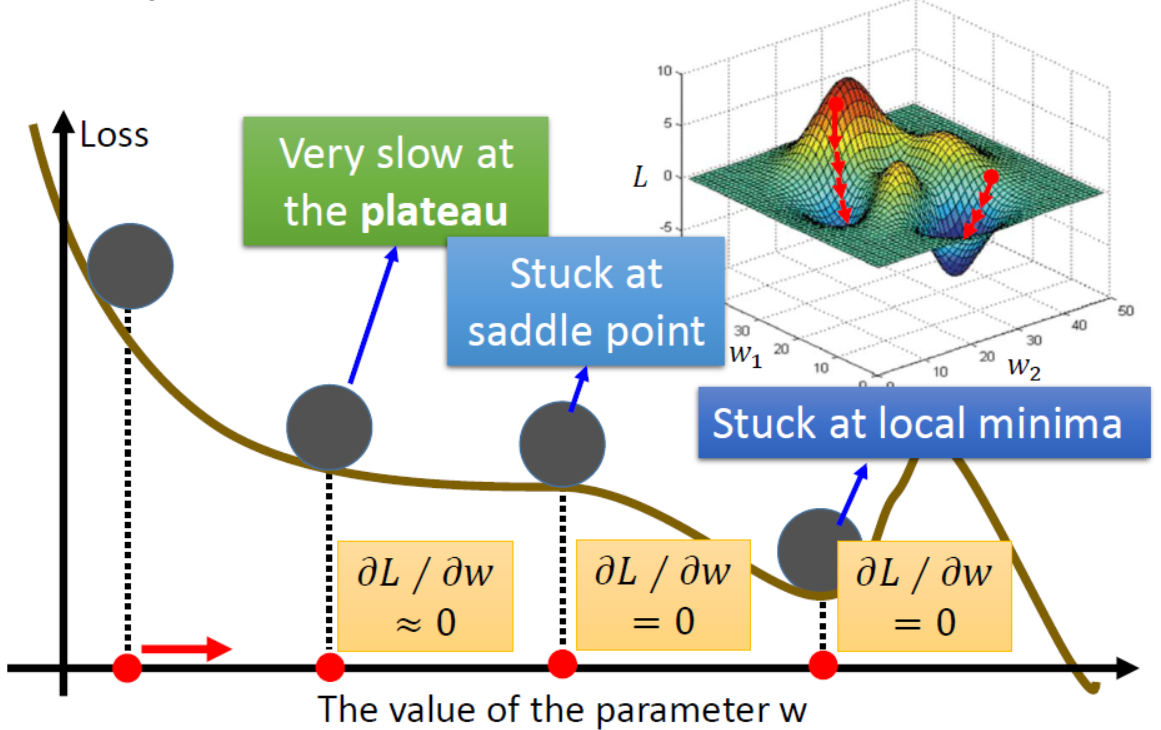
由图可知,经过多次更新参数后,我们不一定能得到最优的参数使得损失函数最小,因为极值点或者驻点不一定函数的最值点。换言之,梯度下降方法容易受初始值$\omega^0$的位置影响而陷入局部最小值。
但幸运的是,在线性回归中,我们的损失函数$L$没有局部最优解。(因为无论是单变量还是多变量的线性回归,损失函数$L$都是凸函数。)
梯度下降法求解
在了解完梯度下降的方法后,利用这个方法来解方程$L(w,b)=\sum_{n=1}^{10}(\hat y^n-(b+wx_{cp}^n))^2$,计算步骤如下。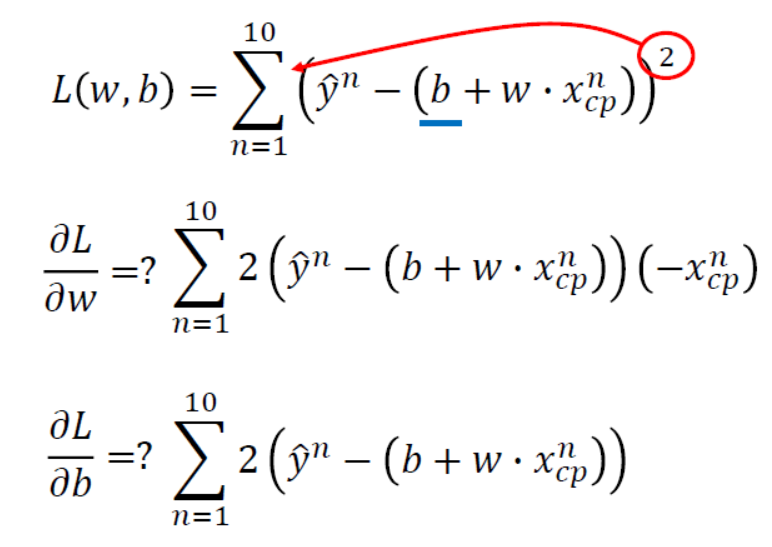
(注:对$b$求偏导最后少了一个$-1$。)
计算结果为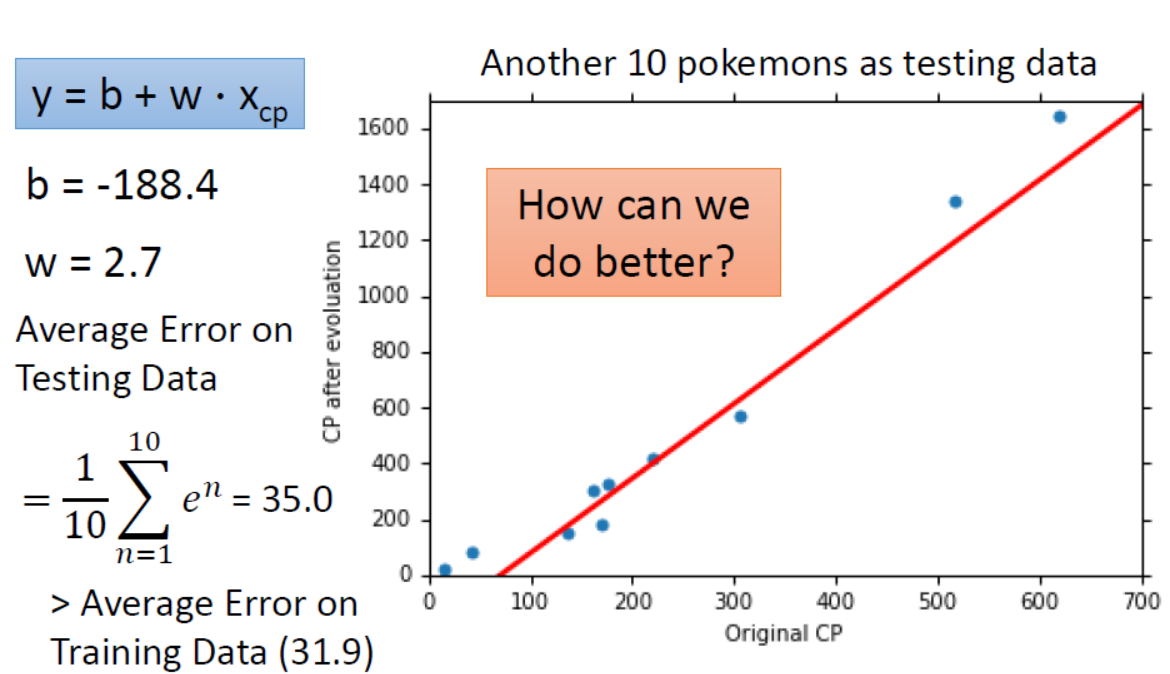
求得的解为$b=-188.4,\omega=2.7$,除此之外,在整个求解过程中我们更关心在测试集上的$Average Error=35.0$,是否可以将其降得更低?
单特征回归模型预测
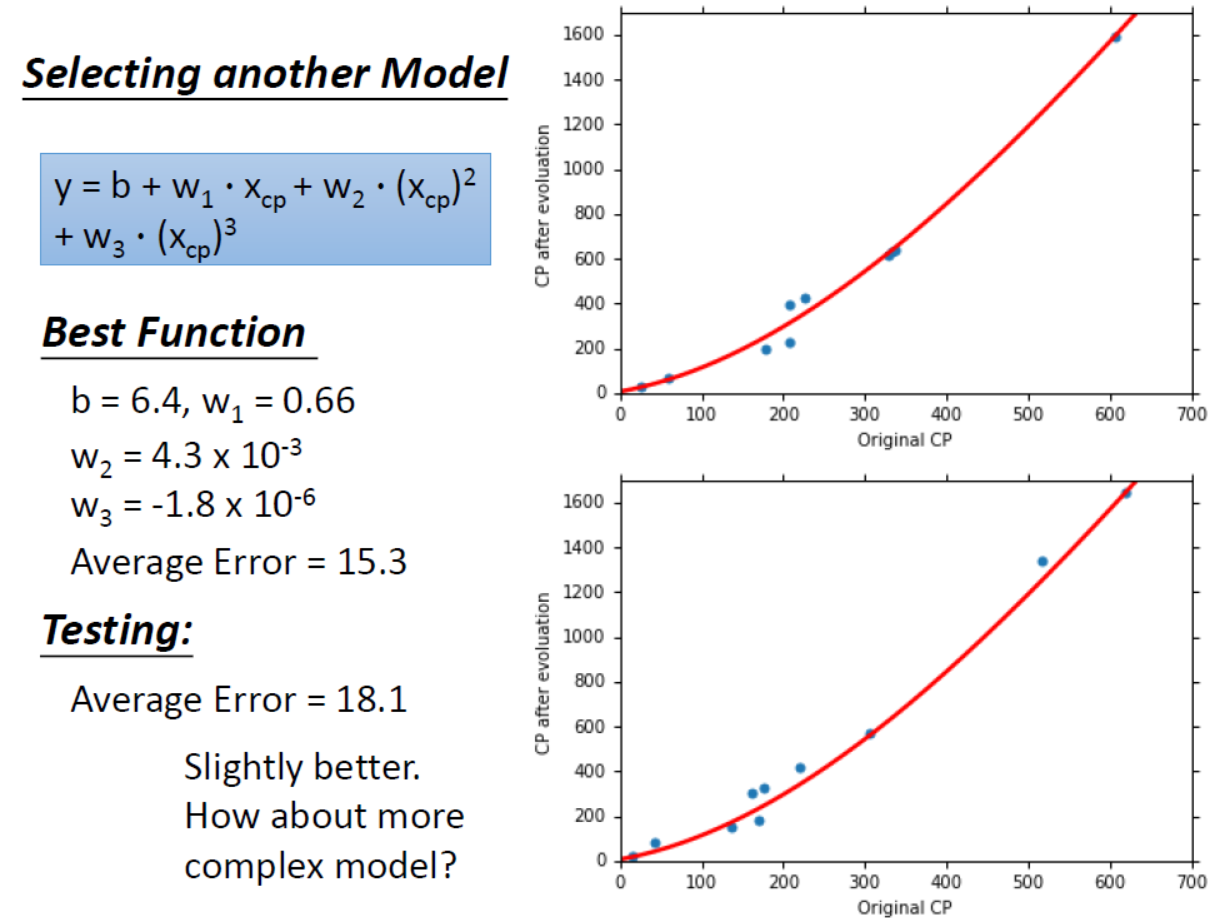
为了让测试集上的$Average Error=35.0$更好地下降,我们可以换用更复杂的模型,即回到第一步建模。将模型进行修改。模型修改后的计算结果如下。(这里补充一点:是不是能画出直线就是线性模型,各种复杂的曲线就是非线性模型? 其实还是线性模型,因为把 $x_{cp}^1 = (x_{cp})^2$ 看作一个特征,那么 $y = b + w_1·x_{cp} + w_2·x_{cp}^1$ 其实就是线性模型。)
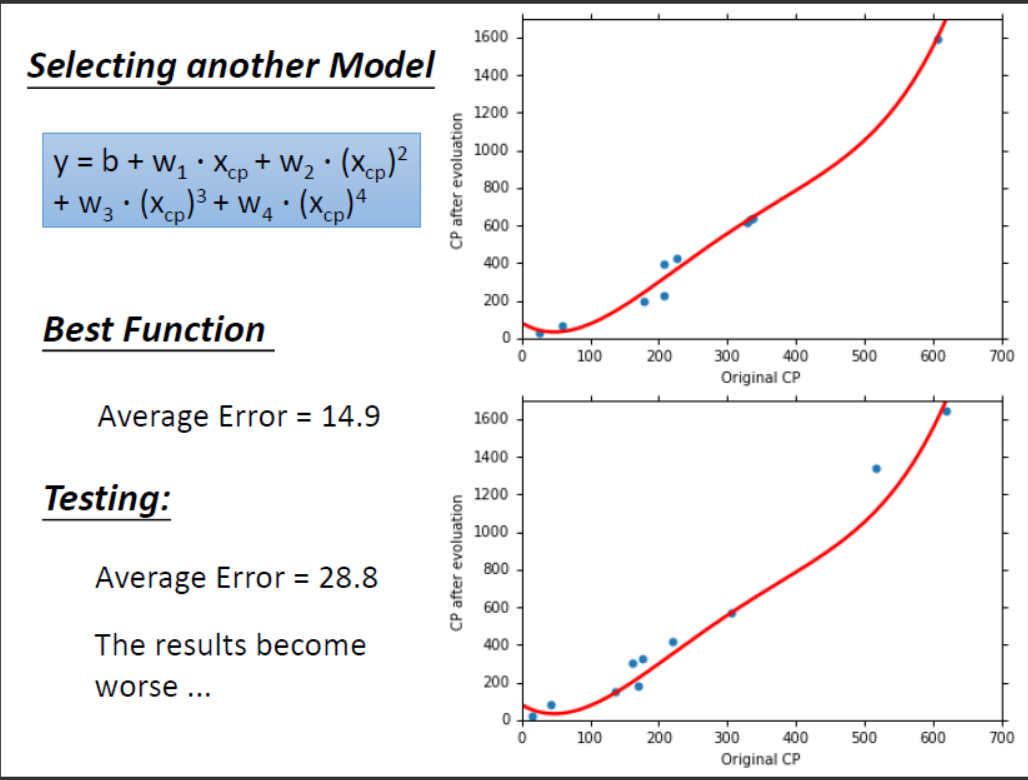


过拟合问题
概念
由上述模型我们得到了一个更好的效果,所以继续增加更高次方的模型。结果如下图所示。

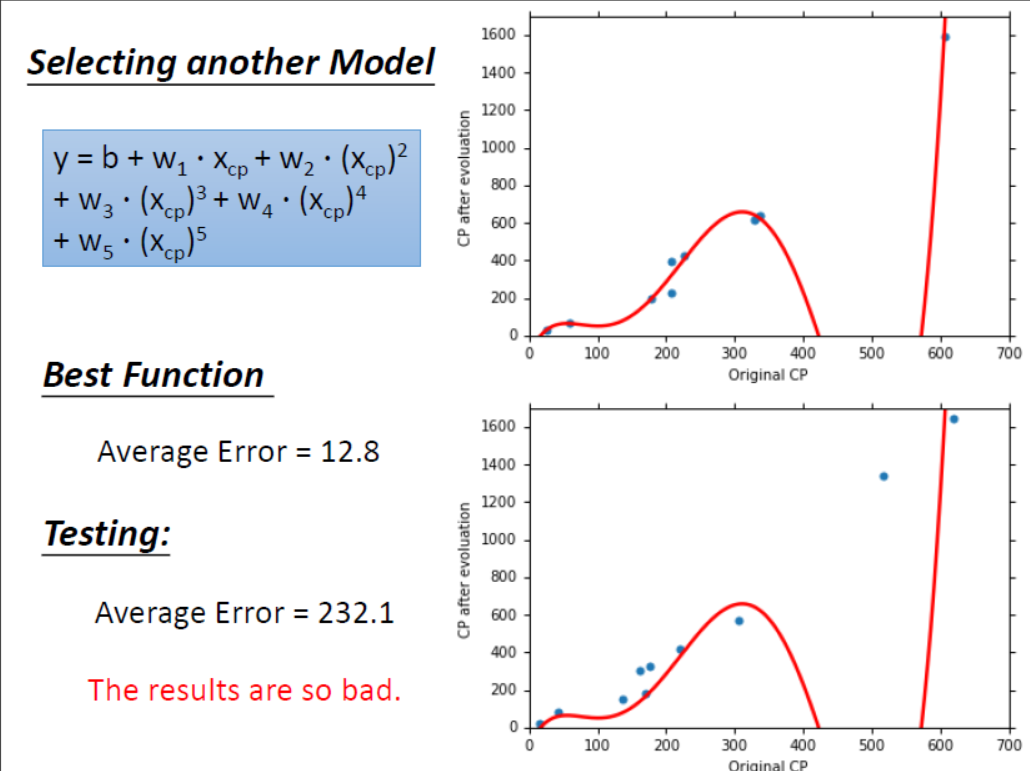
什么是过拟合问题呢?由上图可知,随着模型复杂程度的增加,最终使得模型在训练集上表现的效果更好(训练集上的$Average Error$越来越小)而模型在测试集上结果坏掉的现象称为过拟合(Overfitting)。
过拟合图形化解释
如下所示,假设每一个模型对应一个集合,可得出5次模型 $\supseteq$ 4次模型 $\supseteq$ 3次模型(原因是令高次项的 $w_i=0$ 可得到低次模型)。并且模型越复杂,在测试集上表现效果越好。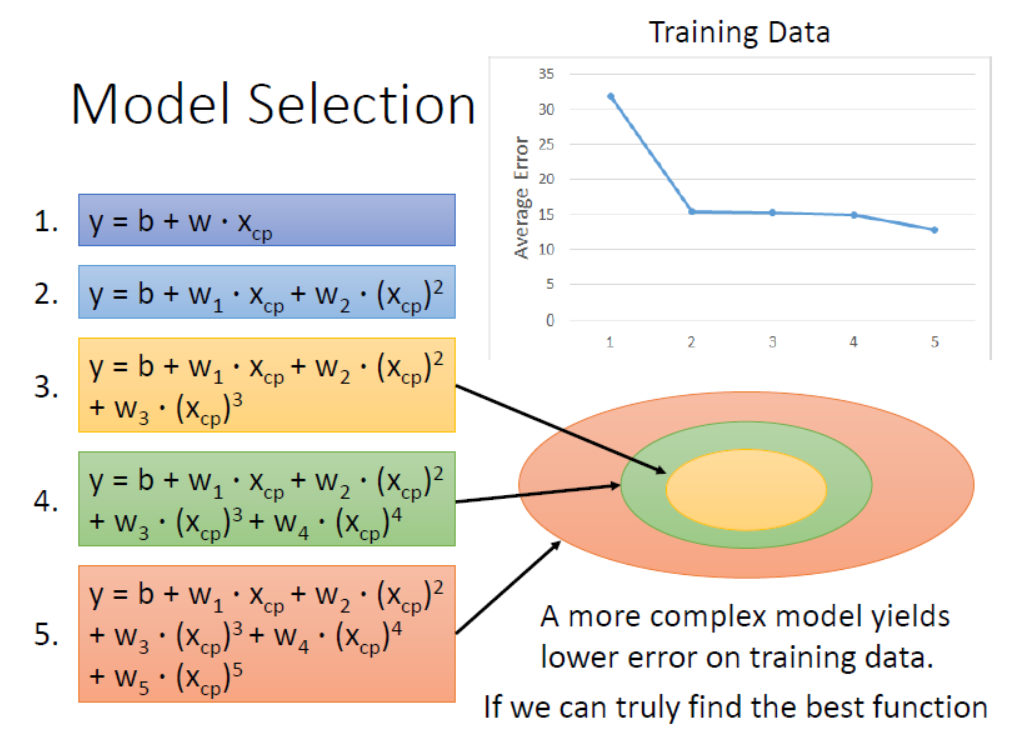
这5个函数在测试集上的表现如下:
发现3次方以上的模型,已经出现了过拟合的现象,并且模型的泛化能力越来越差。所以考虑模型时要同时考虑训练集和测试集上$Average Error$。那么过拟合问题有没有办法解决呢?
正则化解决过拟合问题
解决过拟合问题主要有两种方法,法一是人工决定去掉某些特征(主要是针对引入特征过多造成过拟合),法二是在保留原有特征同时采用正则化(主要针对模型复杂或引入特征过多造成过拟合)。以下主要介绍正则化解决过拟合问题。
正则化概念
正则化是指在保留原有特征的前提下,减小输入参数的幅值影响。做法是在$Loss Function$中加入一个正则化参数$\lambda$,通过它来控制所有输入参数的权重。在本实验中的具体表达式为
$$ L=\sum_{n=1} (\hat y^n-(b+\omega x_{cp}^n))^2+\lambda\sum{(\omega_i^2)} $$
能解决过拟合的原因
过拟合产生的原因是整个模型过于依赖输入参数权值的影响。而正则化的思路是想办法降低参数权值的影响。
对于上述式子,$\lambda$的值可以人为调节。如果$\lambda$很小,那输出效果跟没添加一样。但是随着$\lambda$增大,在求同样的最小$Loss$的条件下,输入参数$\omega_i$的值会相对变小,从而抑制过拟合的产生。并且$\lambda$越大,$\omega_i$越小,拟合曲线越平滑,因为在直线中斜率值越小代表越不陡峭。为什么我们希望曲线越平滑越好呢?
假设模型为$y=b+\sum\omega_i x_i$,当输入一个微小的扰动$\Delta x_i$时,输出为$y=b+\sum\omega_i(x_i+\Delta x_i)$,此时当$\omega_i$的值足够小,则噪声点对于模型的影响就不明显了,从而降低了过拟合。但是如果$\lambda$值一直增大,会使得输出是一根近似于水平的直线,达不到拟合的要求,此时又陷入了“欠拟合”(underfitting)。
正则化的效果
对于同一个模型,进行正则化后调节$\lambda$在训练集和测试集的表现如下。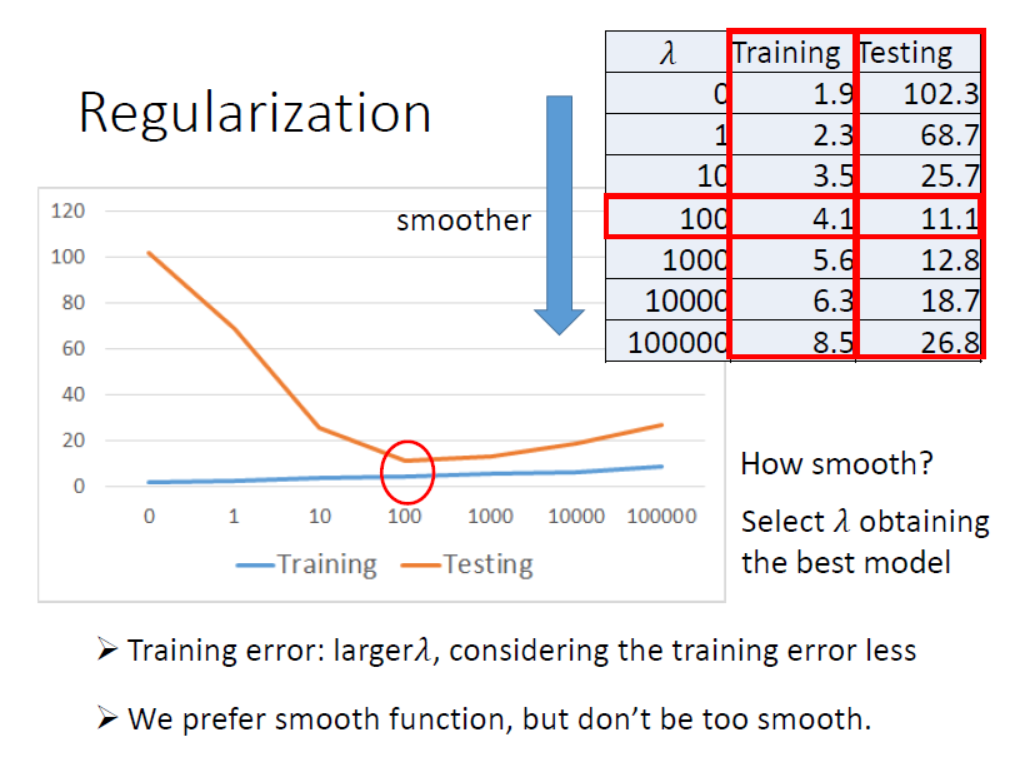
可以看出,随着$\lambda$的值的增加,模型在测试集上的测试误差得到降低的同时训练误差也不会产生太大的变化。此时过拟合问题得到解决。但是当$\lambda$的值超过某一个数值后,测试误差又开始增加,此时又开始陷入了欠拟合。
多特征的回归模型预测
加入宝可梦种类特征
这次我们在实验中抓取了60只宝可梦,它们的数据分布如下图所示。
此时若只考虑宝可梦的初始CP值这一个特征是远远不够的,我们猜测可能还跟宝可梦的种类有关。此时依然采用线性回归得到的模型为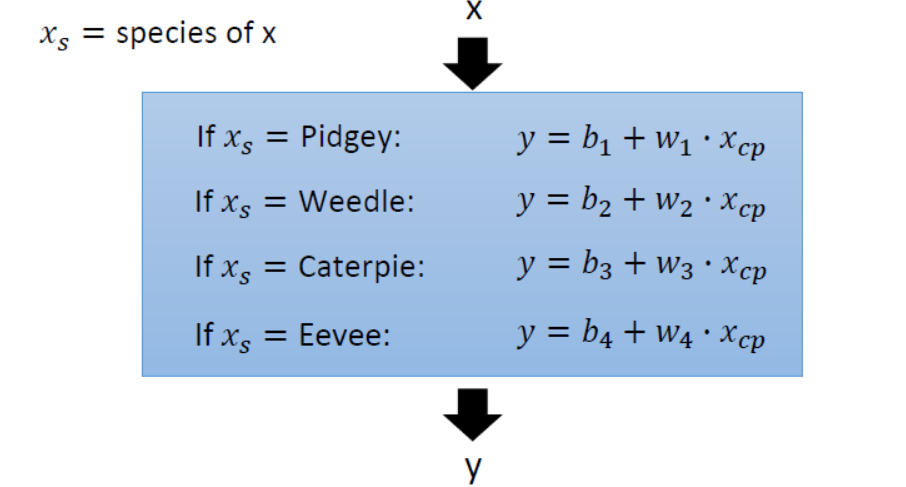
此时又遇到一个新问题,怎样用一个函数将来表示这些不同物种的函数呢?如果你有学过信号与系统的话,就会知道有一个冲激函数$\delta(t-t_0)$,他的含义是当$t=t_0$时函数值为1,其余时刻为0。所以对应地我们这里令$t$等于各个物种即可。
该模型预测的结果为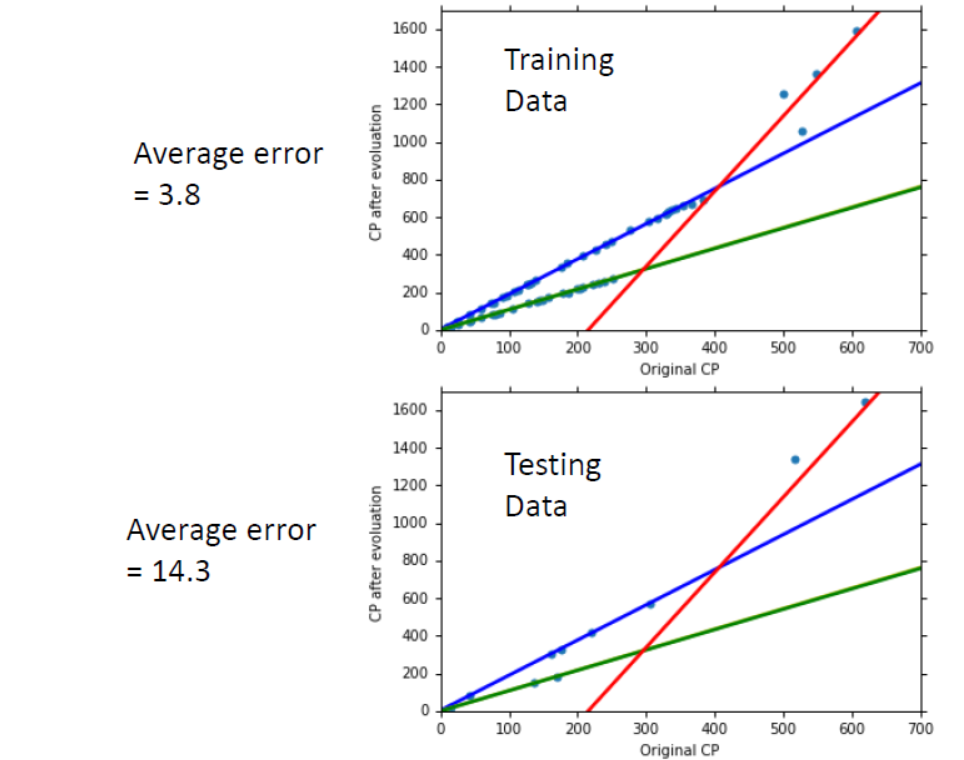
由上图可知,宝可梦按种类划分在训练集上$Average Error$较小,而且预测的结果较为良好。
加入宝可梦更多特征
在上图训练集中,还是有一些值在直线上上下扰动,拟合的不是很好。进化后的CP值会不会还和身高,体重和HP等特征有关呢?在不清楚的情况下,我们考虑把考虑到的特征全添加进去,重新建模如下所示。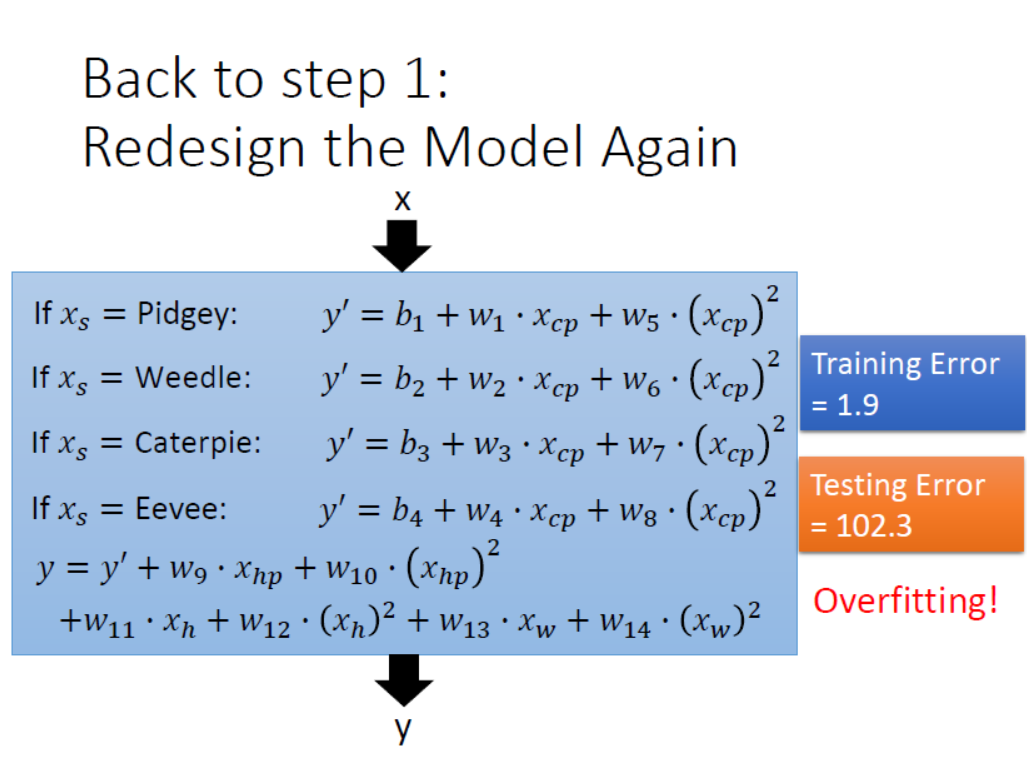
经过计算训练集和测试集上的$Average Error$发现又造成了过拟合,解决方法参考第四点哈哈哈。


