最近导师D说D项目可能可以考虑下流形学习。因此特地去了解下。
流形学习的假设
- 所观测到的数据是高维的,高维数据受数据特征的限制会存在冗余信息,实际上用某个低维向量就能得到唯一表示;
- 高维空间的表示有冗余,映射到低维空间的表示没有冗余,低维空间称为“流形空间”。
举例:在地球仪上计算北京到上海
我们关注地表的距离,而不是三维空间的欧氏距离;
从高维空间上看,北京的坐标是$(x_1,y_1,z_1)$,上海的坐标是$(x_2,y_2,z_2)$,采用空间欧式距离两个点之间的距离是$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$,但是这种方式度量两个城市之间的距离不准确;
把三维的地球展成二维平面,二维平面就是合适的流形空间,此时北京的坐标是$(x_1,y_1)$,上海的坐标是$(x_2,y_2)$,采用空间欧式距离两个点之间的距离是$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$,此时使用欧式距离度量才有意义。
结论
1、只有流形空间上使用欧式距离才有意义;
2、$m$维流形所展开的$n$维空间$(m<n)$不适合使用欧氏距离。
图解二维流形——瑞士卷
假设观测的数据是三维的,在流形空间比在三维空间上做欧氏距离更有意义。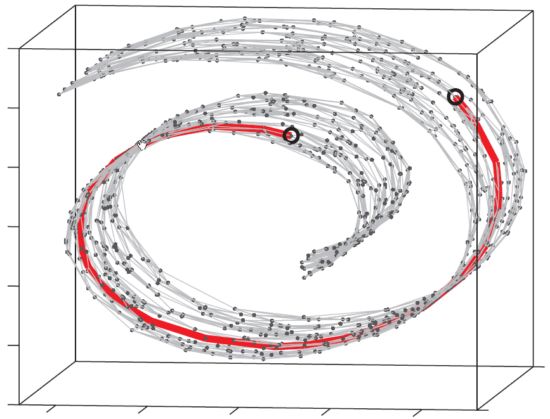
流形学习研究内容
- 在得到模型有效的高维特征表示后,如何实现高维到低维空间的非线性降维,这种降维既能保证能合理使用欧式距离,也能考虑到数据的拓扑结构;
- 如何保证映射的低维空间是流形空间。


