论文题目:HCSC: Hierarchical Contrastive Selective Coding
code:https://github.com/gyfastas/HCSC
Motivation
1、对于Instance-wise的对比学习方法(SimCLR, MoCo, SigSiam等),它们过度关注到实例特征之间的关系,却忽略了整个数据集的语义结构。
2、对于原型对比学习方法,它们更多是在单个层级上做聚类,没有考虑到数据集的多层级的特性。
如下图所示,Instance-wise的对比学习方法更关注的是某个狗的样本和其增扩之间的关系,原型对比学习方法关注的是狗这一类别单个层级的聚类关系,但是实际上狗的类别还能在细分层级,层级下也有对应的原型。
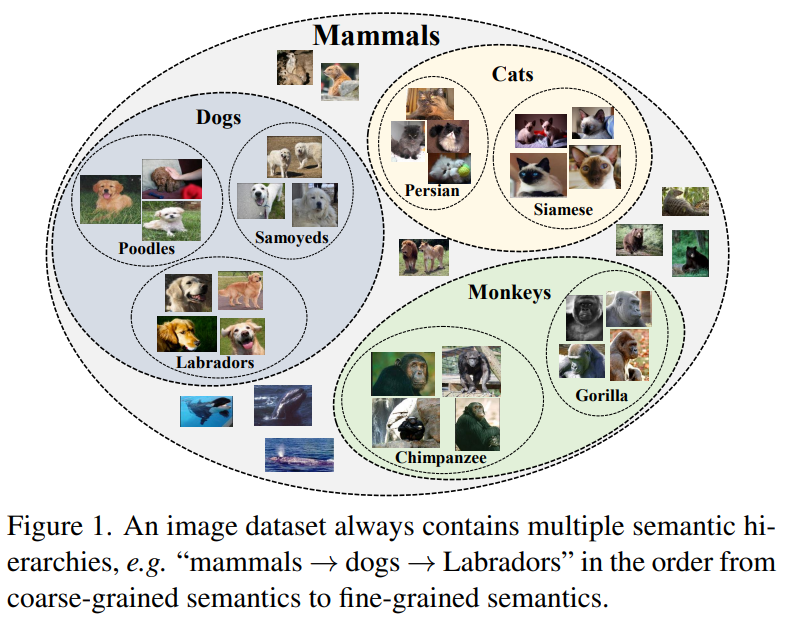
Contribution
1、针对于原型对比学习,本文提出使用分层级的原型来获得数据集的不同层级的语义结构;
2、针对于实例级别对比学习和原型对比学习,根据不同层级的原型在训练时,制定更合适的样本选择和原型选择的策略。在训练时,对于样本的选择,该策略旨在从样本队列中,寻找当前样本所属的原型,和该原型距离最远的相同层级的其他原型群组的样本作为负样本。对于原型的选择,该策略旨在从原型队列中,选择和当前样本所属原型的父亲原型距离最远的原型作为负原型。
问题建模
怎么进行分层级原型的聚类呢?
给定无标签图像$X= \{x_1,x_2,…,x_N \}$,图像经过backbone提取的特征为$Z= \{z_1,z_2…,z_N \}$,其中$x_i\in X$,$z_i \in R^{\delta}$,$i=1,2,…,N$。对于整个数据集,可分为$L$个分级原型,每个分级原型由$M_l$个小原型$c_i$组成,每个小原型$c_i \in R^{\delta}$,$L$个分级原型的集合可定义为$C= [ {\{c_i^l\}_{i=1}^{M_l}} ]_{l=1}^L$。
文中实验是设置$L=3$,每个分级原型的小原型数量分别是$M_1=3000, M_2=2000, M_3=1000$,聚类后原型空间中个数小于10个样本的原型被丢弃。具体可参考下图。
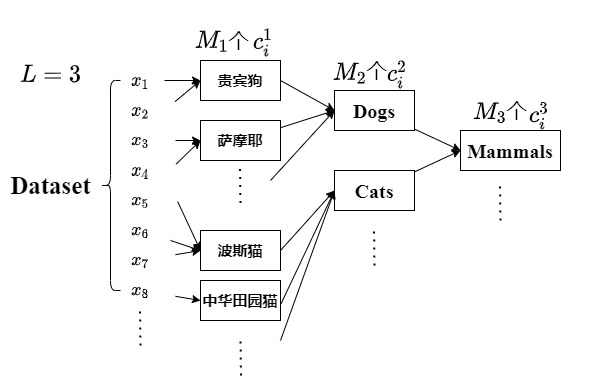
分层的语义表示
文中利用层次聚类算法(Hierarchical K-Means)对$Z=\{z_1,z_2…,z_N\}$来进行分层级聚类。最后利用无向图$Z$将节点连接成树形结构。
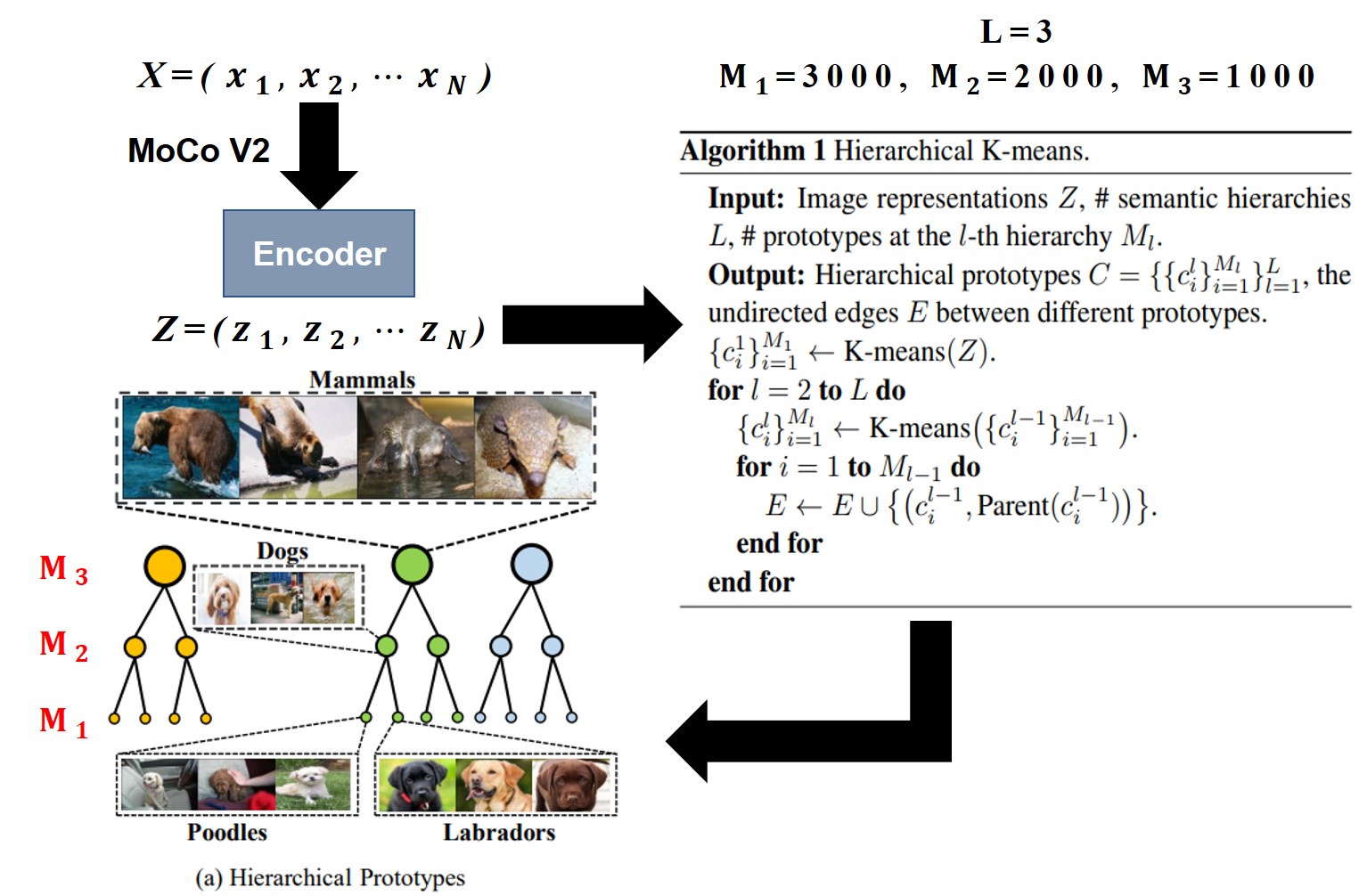
语义表示的结构结果展示如下。
负样本和负原型的选择
特征表示$z$和原型$c$的距离定义为
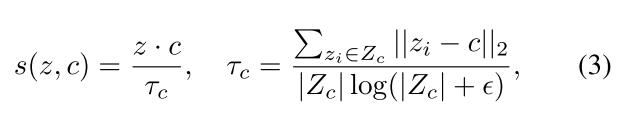
负样本的选择
在相同的层级$l$下,寻找和当前样本$z$所属的原型$c^l(z)$,和该原型距离最远的其他原型群组的样本作为负样本。在队列中的样本$z_j$选择的概率为
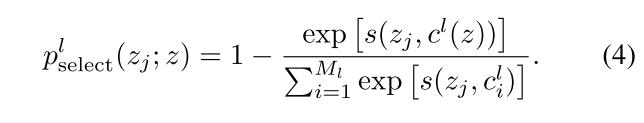
再将上述概率在伯努利分布下进行采样,有下式:
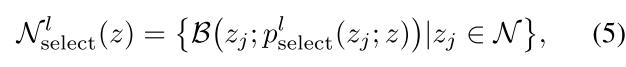
将上述结果带入InfoNCE loss可得下式:
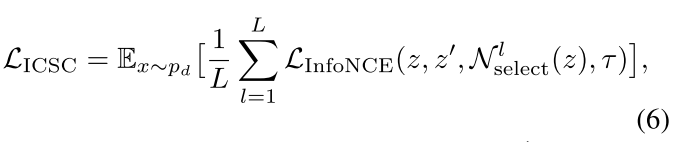
负原型的选择
从原型队列中,选择和当前样本所属原型的父亲原型距离最远的原型作为负原型。
举例来说,对于同一层级下有萨摩耶,贵宾和拉布拉多,萨摩耶和这两类狗的距离更近,和其他父亲原型(猫类)的子原型(波斯猫等)距离更远。所以负原型应该从其他父亲原型的子原型中选择。在队列中的原型$c_j$被选择的概率为
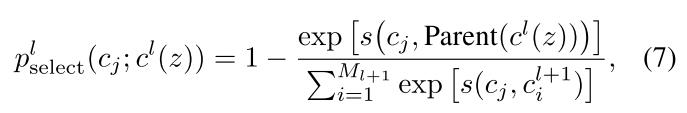
再将上述概率在伯努利分布下进行采样,有下式: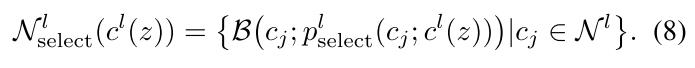
将上述结果带入ProtoNCE loss可得下式:
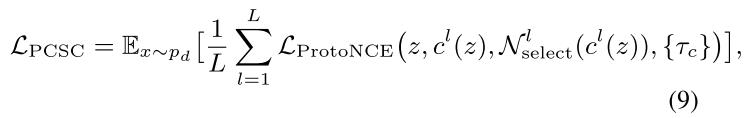
通过上述两种负样本和负原型的选择策略,得到如下结果。

存在的问题
1、对于数据集的所分的层级是敏感的;
2、对于原型的数量也是敏感的。


