论文题目:Prototypical Contrastive Learning of Unsupervised Representations
code: https://github.com/salesforce/PCL
Motivation
如今自监督对比学习的经典做法离不开数据增扩和对比损失,针对于对比损失而言,在batch里面划分正负样本的做法会忽视数据的语义结构表示,许多具有相似语义结构的负样本实例在特征空间其实不希望被拉开距离,但是对比损失会放大他们之间的差距。
Contribution
1、在自监督对比学习的特征空间引入聚类,聚类希望语义相似的负样本实例约束在同一个原型群组中,不会因为对比损失而拉大差距;
2、提出原型的概念,一个原型是指相似语义结构的特征表示聚在一个群组(图中的圆)中的embedding;即使是负样本,语义结构相似的应该属于同一群组(同一个圆内)。
3、为了估计每个原型群组中的特征分布,文章把泛化InfoNCE loss为ProtoNCE loss;
4、将整个数据集的图像分配给不同粒度的多个原型群组。
图中绿框表示粗粒度的原型群组,原型是绿点,只要是有马都归在这个原型群组中,人马也属于该原型群组中的一个细粒度的原型群组(图中左边的蓝框)。
图中两个蓝框表示在细粒度的原型群组中,负样本会给约束在原型空间中,而不是单纯被InfoNCE loss拉远。
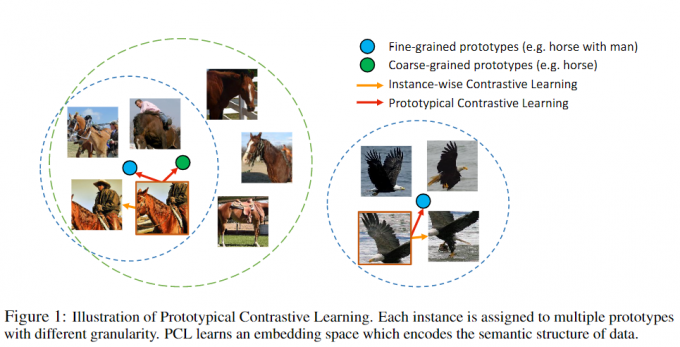
做法
极大似然估计
多数情况下我们是根据输入样本和模型参数来推算结果,而极大似然估计是已知输入样本及其服从的分布,然后寻求使该结果出现的可能性最大的条件,以此来估计参数。附上极大似然估计讲解。
EM算法
EM算法主要解决在极大似然估计中,输入数据的概率分布未知的问题,通过引入隐变量$𝒛$的分布,方便对参数$\theta$进行极大似然估计。
附上EM算法讲解。
- E Step:隐变量的条件概率分布的期望的求解——根据当前的模型参数$\theta^{(i)}$和观测数据$X$求得隐变量的条件概率分布期望$Q(z^{(i)})$;
- M Step:参数的求解——根据$Q(z^{(i)})$求参数$\theta^{(i)}$的似然函数,通过取对数求导,令导数等于0得到模型参数$\theta^{(i+1)}$。
重复上述操作。直到$\theta$收敛。
训练过程如下:
采用MoCo的架构,把原型的embedding当成隐变量$C=\{c_i\}_{i=1}^k$,通过E step可得到$Q(c_i) = p(c_i;x_i,\theta)$,通过M step求得网络参数$\theta^\star$,整个训练的损失函数为
$$L_{ProtoNCE}=L_{infoNCE} + L_{Proto}$$
网络参数具体求解
建议看完极大似然估计讲解再往下看。
给定训练集$X={x_1,x_2,…,x_n}$,之前对比学习的做法是将$X$映射到$V={v_1,v_2,…,v_n}$,再使用如下对比损失进行优化求参数。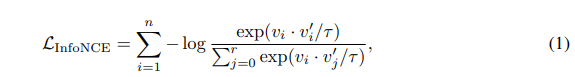
在原型对比学习中,用原型$c$当成隐变量,代替特征$v^{\prime}$,温度系数被替换成为原型浓度估计$\phi$。
$n$张图像的极大似然估计为
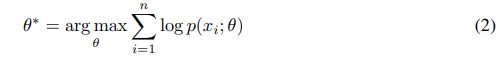
引入隐变量$C=\{c_i\}_{i=1}^k$,有
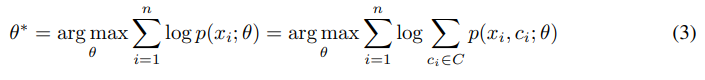
假设$Q(c_i)$是原型$c$的分布,上式经过Jensen不等式和丢弃常数项的操作后可优化为
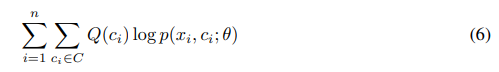
E step
目的是得到$p(c_i,x_i;\theta)$的期望。Momentum encoder输出特征$v_i^{\prime}=f_{\theta^\prime}(x_i)$在$p(c_i,x_i;\theta)$的分布下使用K-means算法,可以得到$k$个聚类中心。$x_i\in c_i$输出1,否则0。
M step
目的是求解参数$\theta$。
当且仅当$Q(c_i)=p(x_i,c_i;\theta)$时,(6)式有最大下界。可得下式。
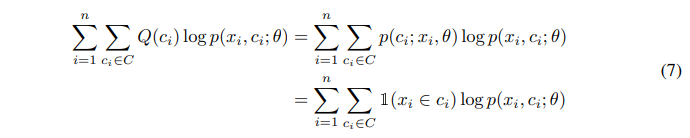
假设聚类的质心是均匀的,有下式。
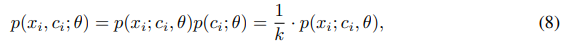
为求解参数,再假设每个原型的分布是各项均匀的高斯分布,有
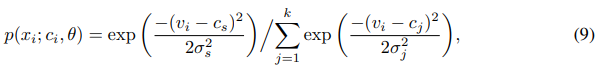
可解得网络参数为
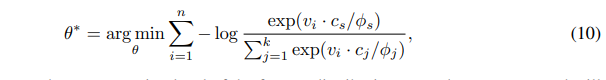
上述是聚类算法的网络参数解法。联合对比学习损失函数可得下式。
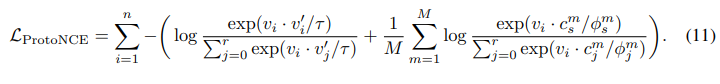
浓度系数估计
系数$\phi$反映原型群组聚集的紧密程度,$\phi$越小表示群组越小,且聚合度高。用于衡量特征$v_z^\prime$和对应原型$c$之间的相似度。定义为
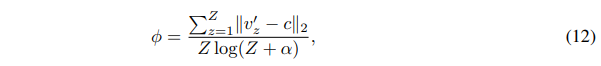
momentum编码器的输出特征为$\{v_z^{\prime}\}_{z=1}^Z$。
实验结果
TSNE图
在ImageNet上训练前40类的TSNE图。

粗细粒度分类展示
绿框和黄框表示聚类结果(粗粒度的原型),绿框属于聚类结果中更细粒度的原型。像在马的粗粒度原型中,人和马就是细粒度的原型。换句话说,在马的类别,含有人马之间的图像距离更近。



