关于机器学习的入门课，个人感觉没太多新东西，只是当时有空就顺便写下哈哈哈，其实这些基础概念知乎博客应该比比皆是，但是我既然写过了不放上博客感觉自己好像白写了，呜呜呜。放上面有时候自己看看也有点小成就感(￣︶￣*))

机器学习拟合的误差来源

误差来源

为什么我们要了解机器学习拟合的误差的来源呢？因为只有从源头上把握误差的产生，我们才能更好的调整模型参数，进一步从训练集中找到一个估测函数$f^*$，使它无限接近于原问题的目标函数$\hat f$。然而使得估测函数$f^*$与目标函数$\hat f$存在差距的来源是偏差（bias）和方差（variance）。

偏差和方差

概念

偏差（bias）描述的是在测试集上拟合出来的模型输出的均值与样本真实期望的距离。简言之。就是拟合出来的模型在测试集上表现好不好。方差（variance）描述的是模型每次输出结果与输出期望之间的误差，简言之，就是测试数据在模型上的离散程度。

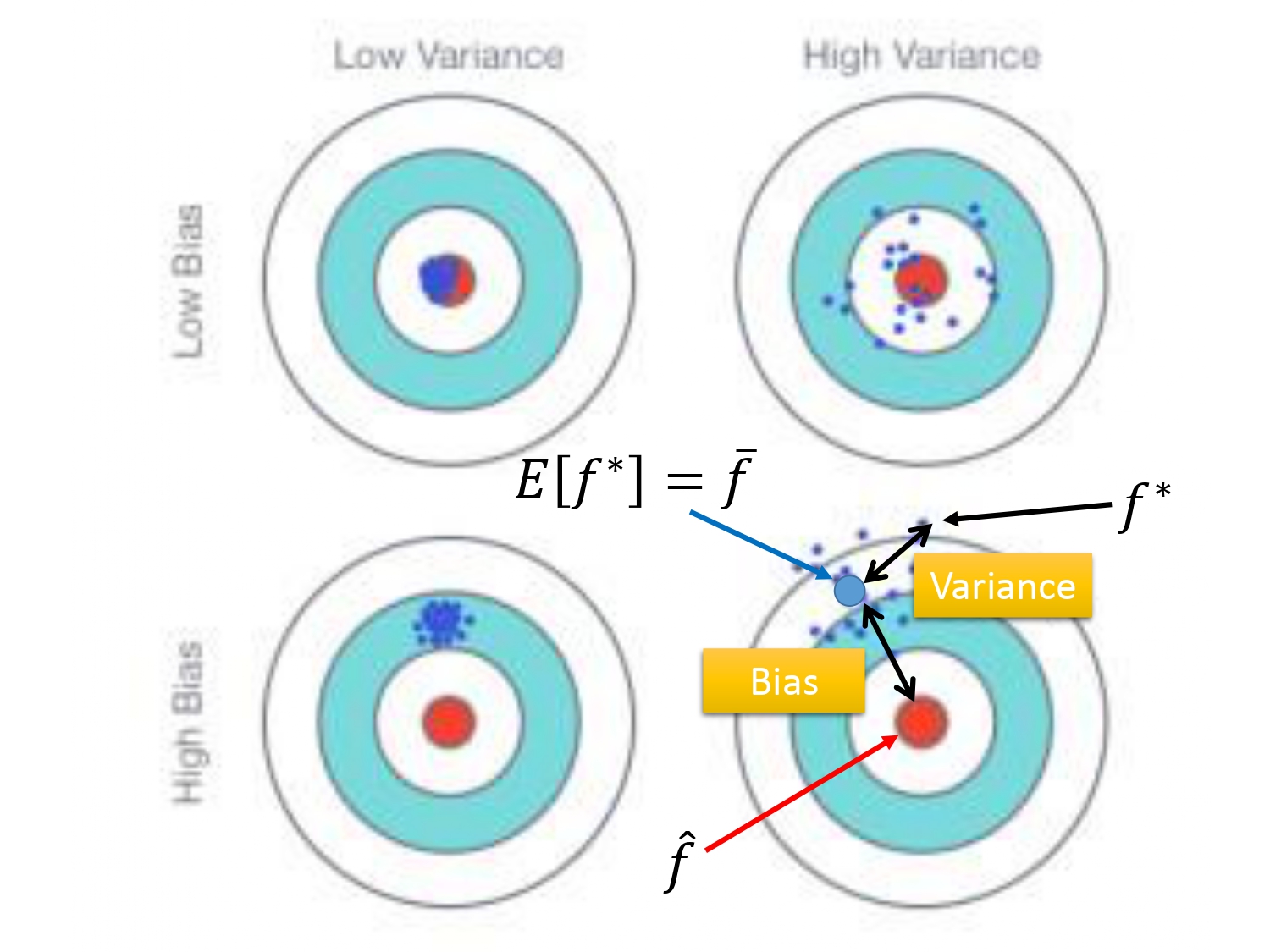
如下图所示。如果以射靶为例子的话，样本的真实结果就是你瞄准的红心（目标函数$f^*$）,像第四个图，偏差就表示模型输出结果的期望和真实结果之间的距离，偏差越大，表示输出数据整体上远离目标函数，就根本没有瞄准靶心打（像第三和第四个图）；偏差越小，表示输出数据靠近目标函数，是瞄准靶心打的。方差越大，表示输出的结果相对于输出结果的均值很分散，方差越小，表示输出结果相对于输出结果的均值较为集中。

所以就会出现以下四种情况——瞄准了打的也很集中，瞄准了但可能由于手不稳定打的很分散，根本没瞄准但手稳定打的也很集中，根本没瞄准且手也不稳定打的很分散。

均值和方差的估算

讨论方差的估算可以理解，那为什么要讨论均值的估算呢？因为只有先估算出采样数据的均值，我们才能更好地计算偏差（数据均值和目标函数期望值的距离）。

假设变量$x$的均值为$\mu$，方差为$\sigma^2$。为了估算出这两个值，我们对变量$x$进行了$N$次采样，计算$N$次的平均值$m$其实并不等于$\mu$（除非进行无限点的划分），$m$的值会$\mu$上下波动，但是我们可以通过这$N$个点的期望去计算出$\mu$。这种估计叫无偏估计（unbiased estimator）。

那我们怎么衡量$N$个采样点对于均值$\mu$的离散情况呢？可以采用以下公式计算$var[m]$，其中可见$N$值越大代表数据越集中，越小代表数据越分散。

以上就是均值的估算，方差的估计可以采用以下公式。通过$N$次有限次采样的值可计算得到一个$s^2$，我们可以使用$s^2$去估计$\sigma^2$，通过计算$E(s^2)$我们发现并不恰好等于$\sigma^2$，这种估计叫有偏估计(biased estimator)。

可以看出，采样次数$N$越大，$s^2$与$\sigma^2$之间估测的差距会减小。

模型复杂度的影响

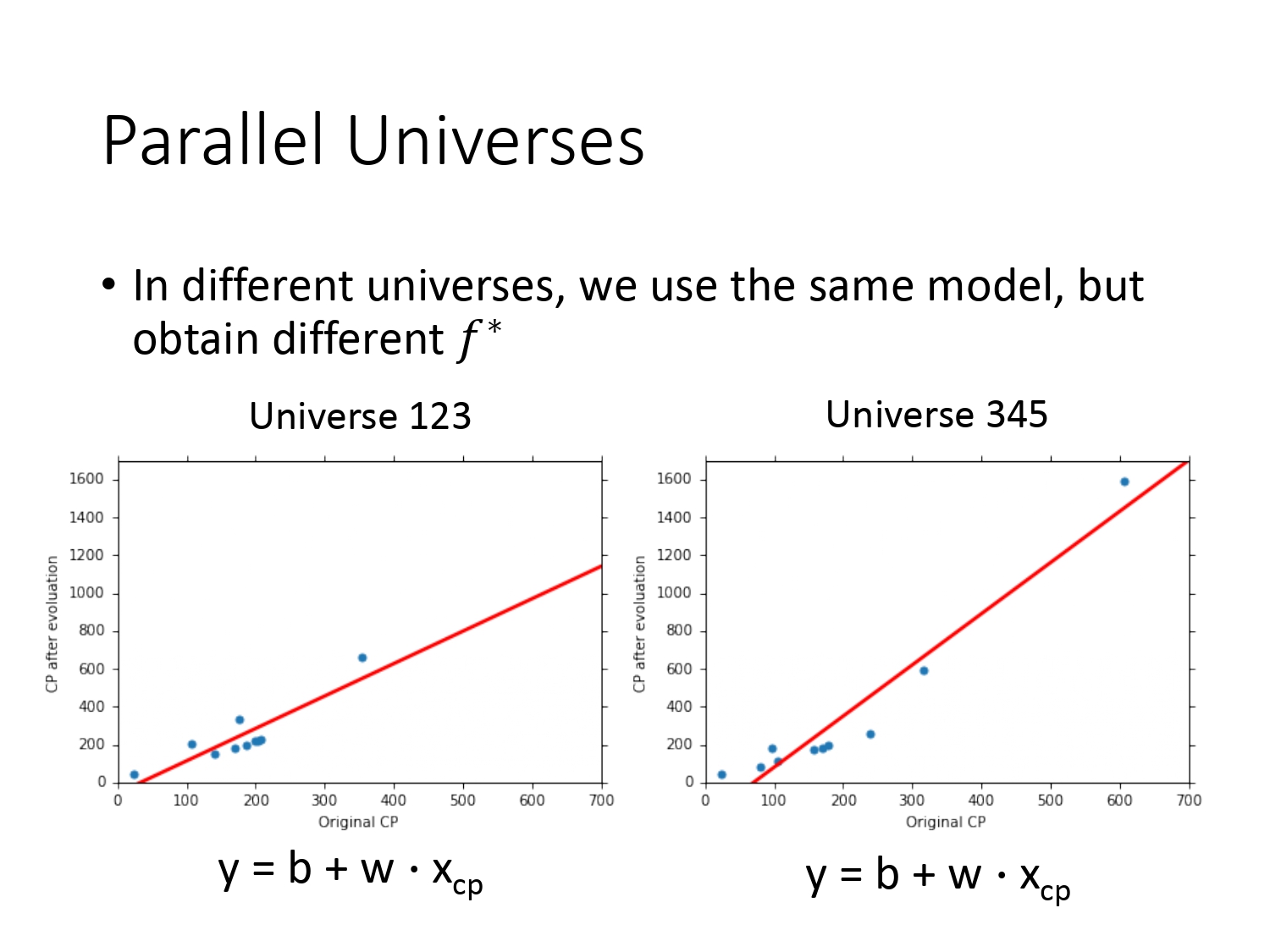
在Regrssion宝可梦的案例中，我们只训练得到了一个函数，但是实际上我们需要得到足够多的函数再取均值才能知道偏差的大小。所以在宝可梦的案例中，我们假设有很多个平行宇宙，如下图所示，并且在这些宇宙上抓10只宝可梦去训练同一个模型，可得到不同的函数，可以求得函数的均值。但现实生活可能不存在平行宇宙，此时可理解为同时进行了多次实验，并且将实验中的数据同时用同一模型去求得不同的函数。

由于平行宇宙中宝可梦的数据不同，使用同一模型得到的$f^*$也不同。如下图所示。

为了说明模型复杂度对方差的影响，我们对于100个平行世界的数据，使用了复杂度不同的三个模型，得到结果如下。

不同模型对方差的影响

方差主要看的是训练数据在模型上的离散程度。由上图可以得出以下结论：

对于不同模型的方差，由一次模型的训练数据比较集中，五次模型的训练数据比较分散，可以得出越简单的模型，方差是越小（因为模型越简单越不容易受训练集的影响），越复杂的模型，方差越大。

不同模型对偏差的影响

偏差要看的模型的均值和目标函数的期望的距离。问题来了，在宝可梦的案例中，我们无法得知具体的目标函数。所以我们的做法是假设一个最佳函数$\hat f$（如下图黑线所示），通过该函数生成一系列数据模拟宝可梦的数据，再进行采样，利用采样数据去训练模型。

为了说明模型复杂度对偏差的影响，我们对于5000个平行世界的数据，使用了复杂度不同的三个模型，得到结果如下。

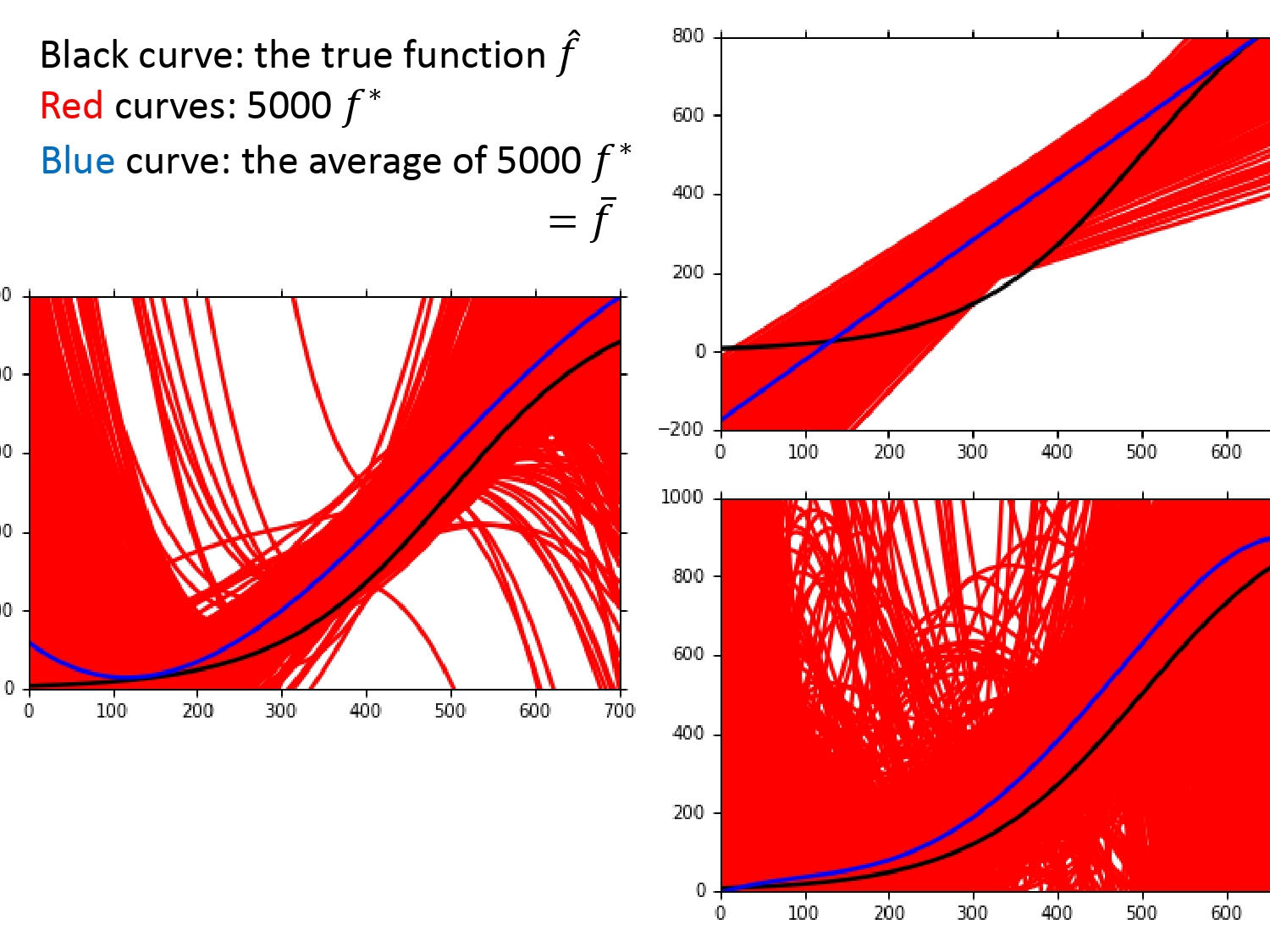
由上图可以得出以下结论：

对于不同模型的偏差，由一次模型的均值（蓝线）和目标函数差的很多，五次模型均值（蓝线）和目标函数差的较小，可以得出越简单的模型，偏差越大，越复杂的模型，偏差越小。

产生影响的原因

为什么不同复杂情况的模型会对方差和偏差产生这样的影响呢？

如下图所示。假设所有的解函数和目标函数都在集合中。

如果模型比较简单，解函数的集合会比较小，此时数据也比较集中，但可能解集合中不包含目标函数，此时我们看到的就是偏差大，方差小的情况。如果模型比较复杂，解函数的集合会比较大（复杂模型可通过参数设置转化为简单模型，故解函数集合较大），此时数据会比较分散，但可能解集合中一般包含目标函数，此时我们看到的就是偏差小，方差大的情况。

造成影响的后果和解决方法

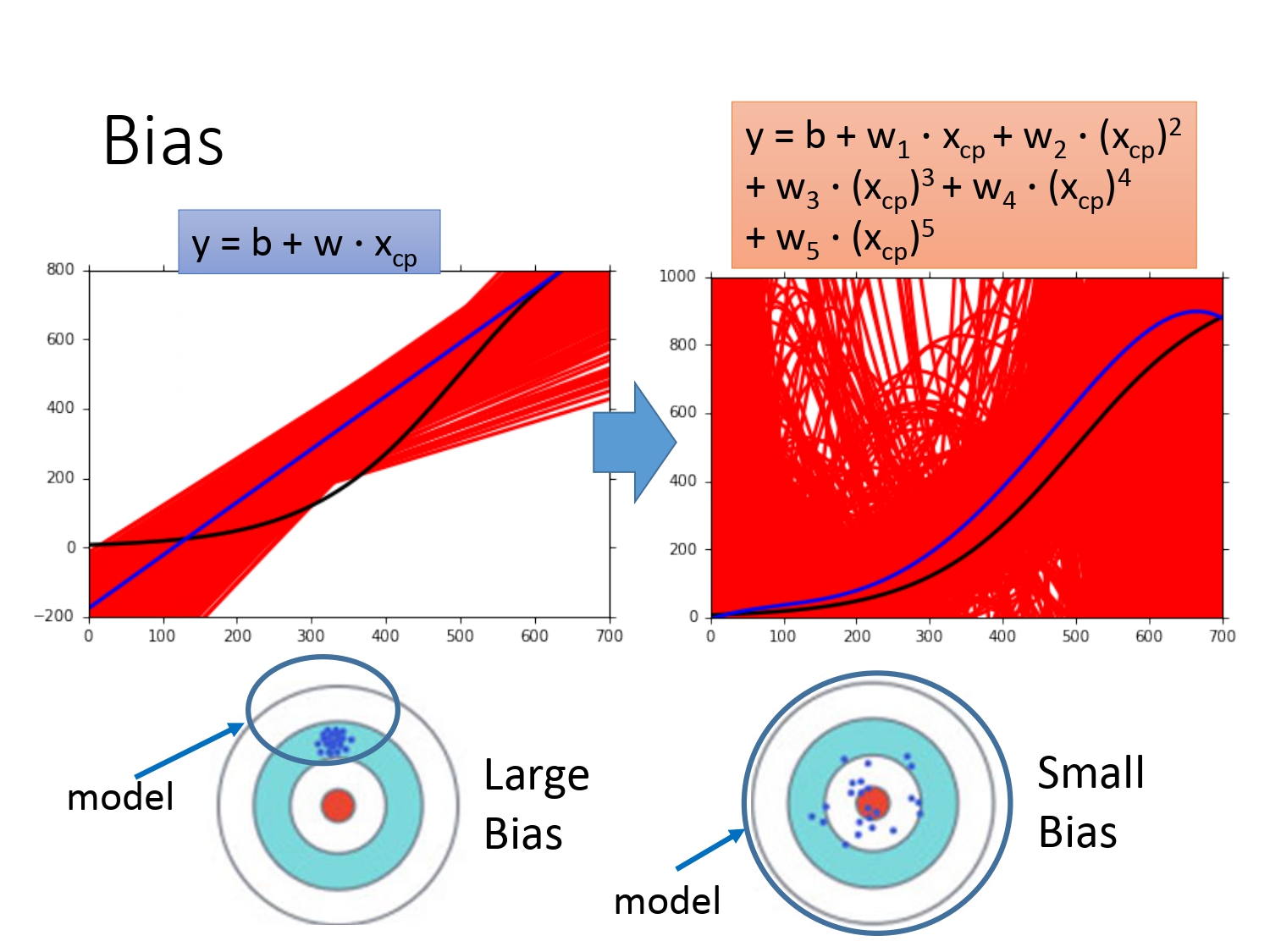
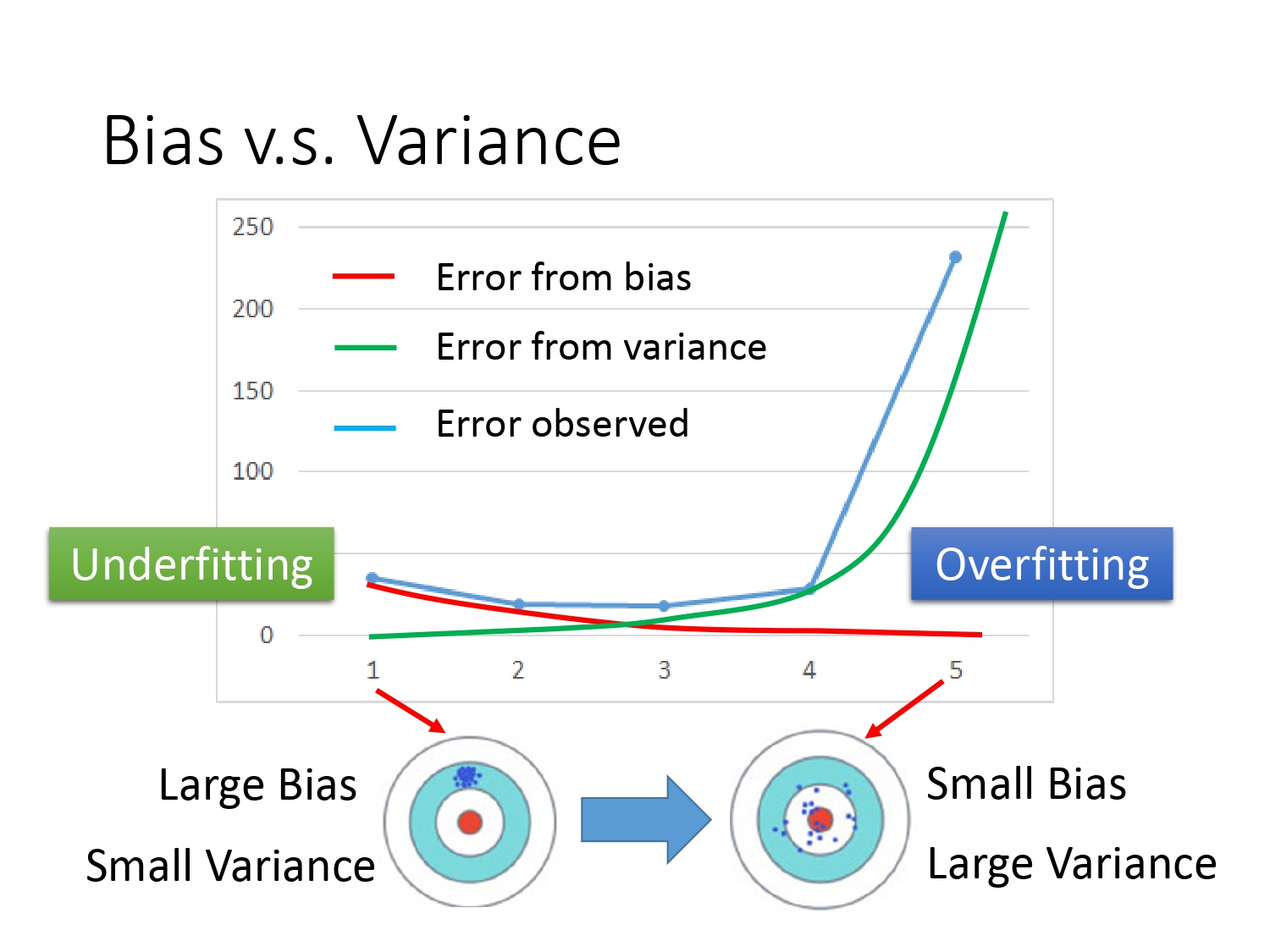
通过以下曲线图，我们可以看出模型越简单，意味着偏差越大，造成的后果是欠拟合。具体表现是模型在训练集上的误差较大。解决欠拟合问题一般的思路有两个。

模型增加更多的输入特征；
换一个更复杂的模型。

模型越复杂，意味着方差越大，造成的后果是过拟合。具体表现是模型在测试集上的误差较大。解决过拟合问题一般的思路也有两个。

增加训练数据；（因为方差大的表现是数据分散，增加数据能相对提高集中度，但实际操作数据难获取）
采用正则化。（加个惩罚项使得输入参数的影响尽量小，曲线尽量光滑，具体做法参考Regression）

模型的选择

通过模型复杂度的影响我们可以看出，偏差和方差之间是相互制衡的，具体可通过一个模型来表现。那怎么选择出一个好的模型呢？如下图所示，我们能否简单地认为在已有的测试集上$Error$最小的模型表现一定是最好的呢？

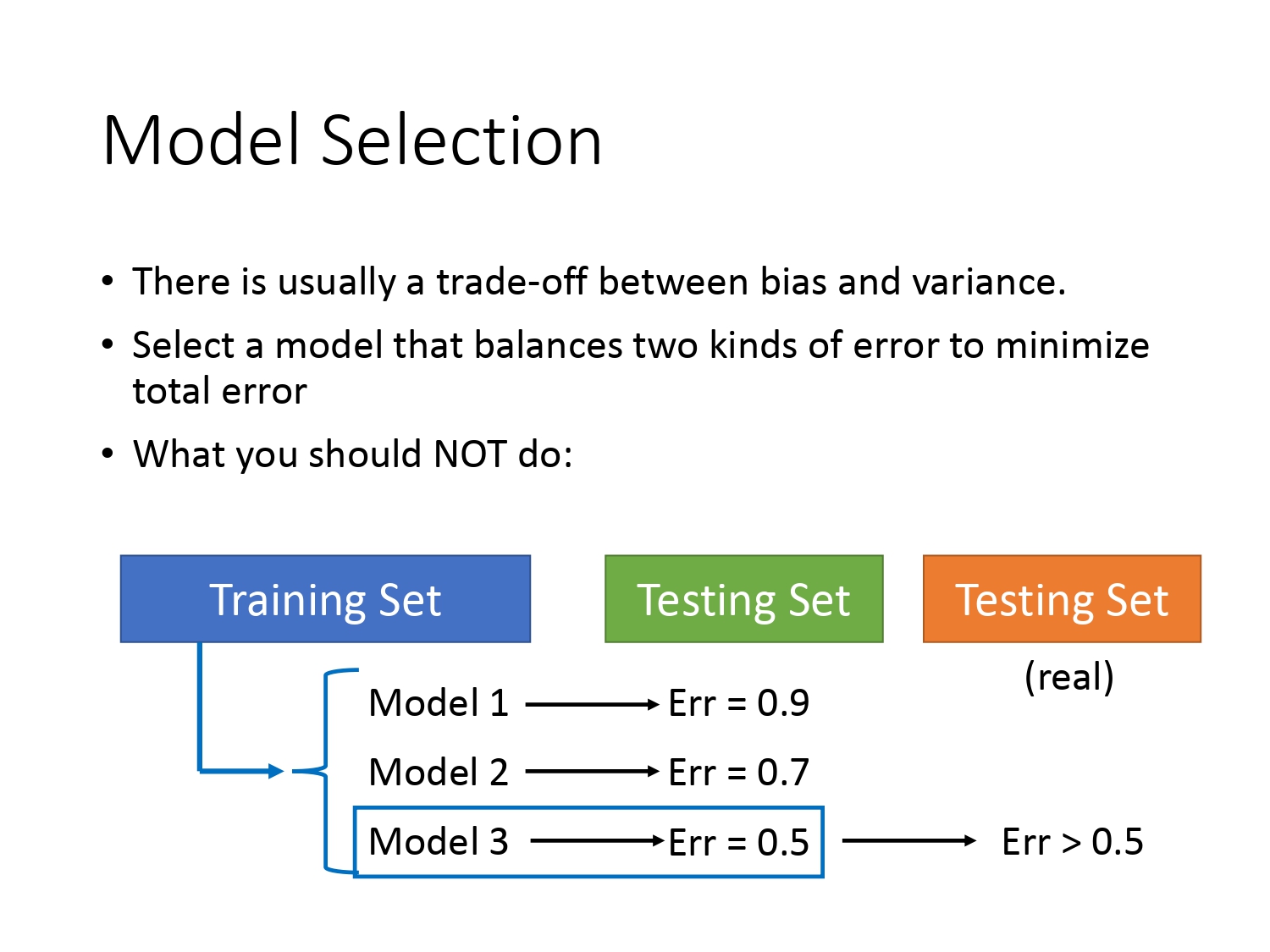
其实这种想法不正确，往往在未知测试集上得到的结果是大于你之前测得的结果。这个时候你总不能回头再调节模型的参数让他在测试集上表现的更好吧。回头调节的危害是相当于你把测试集当成训练集用，在测试集上表现好的同时也容易产生过拟合。当实际部署到应用时泛化能力会很差。

就好比你今年参加高考，你可以不断地利用模拟题或往年真题去寻找知识漏洞，但是你总不能用今年的高考试题去进行知识捡漏，假设你考试前真的做到一模一样的试题，那你确实可以考得很好，但万一试题产生较大变动，可能结果会差强人意。所以正确的做法是在测试前一旦确定了模型，最好不要再改动。

交叉验证

概念

既然不能利用测试集进行调参，那怎样做比较合理呢？俗话说“解铃还须系铃人”，我们又回到了训练集，将训练集的数据按照一定的比例分为训练集和验证集，在训练集上训练出模型，通过验证集去选择误差最小的模型。这就是交叉验证（Cross Validation）。换言之，将准考考试的资料（训练集）划分一部分出来当作模拟考试（验证集）用，寻找知识漏洞。这才是常规做法。而最后的高考（测试集）只有一次。（目的是检测模型的泛化能力）

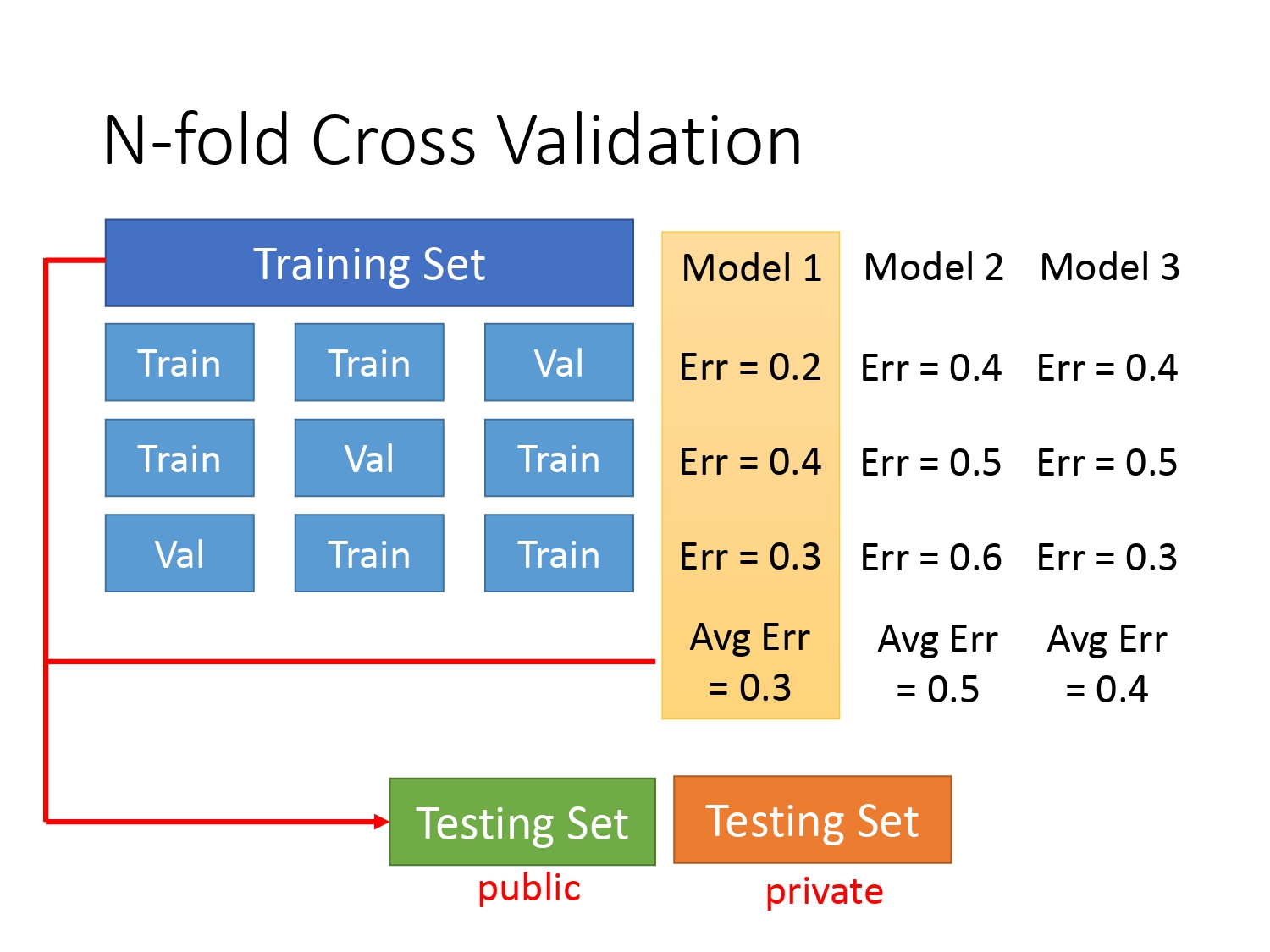
N折交叉验证

既然已经确定了将训练集分成训练集和验证集，那怎样的分法比较好呢？有一种方法叫N折交叉验证（N-fold Cross Validation）。它是指将整个训练集分为$N$份，然后最后一份作为验证集，前$N-1$份作为训练集；倒数第二份作为验证集，剩下$N-1$作为训练集；…；一直到第一份作为验证集，剩下$N-1$份作为训练集。（总共有$N$份验证集，每份验证集对应着$N-1$份训练集）再用不同模型去进行$N$次训练，最终选择一个平均误差最小的模型。下图以$N=3$为例。